- 415.50 KB
- 2024-02-28 发布
www.ks5u.com
2016-2017学年度第二学期
汪清六中期中考试高二理科数学试题
总分:150分 时量:120分钟
班级: 姓名:
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.)
1、若复数的实部与虚部是互为相反数,则的值为( )
A.-2 B.2 C.- D.
2、与向量a=(1,-3,2)平行的一个向量的坐标是( )
A. B.(-1,-3,2) C. D.
3、已知,若,则的值等于( )
A. B. C. D.
4、已知复数(a∈R)在复平面内对应的点位于第二象限,且|z|=2,则复数z等于( )
A.-1+i B.1+i C.-1+i或1+i D.-2+i
5、下列函数中,导函数是奇函数的是( )
A. B. C. D.
6、等轴双曲线的一个焦点是(-6,0),则它的标准方程是( )
A. B. C. D.
7、以双曲线的右顶点为焦点的抛物线的标准方程为( )
A.=16x B.=-16x C.=8x D.=-8x
8、已知△ABC的三个顶点为A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的中线长为( )
A.2 B.3 C.4 D.5
9、设函数f(x)在点附近有定义,且有,(a,b为常数),则 ( )
A.f′(x)=a B.f′(x)=b C.f′(x0)=b D.f′(x0)=a
10、若椭圆(a>b>0)的离心率为,则双曲线的离心率为( )
A. B. C. D.
11、双曲线的实轴长与虚轴长之和等于其焦距的倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为( )
A.-=1 B.-=1 C. -=1 D.-=1
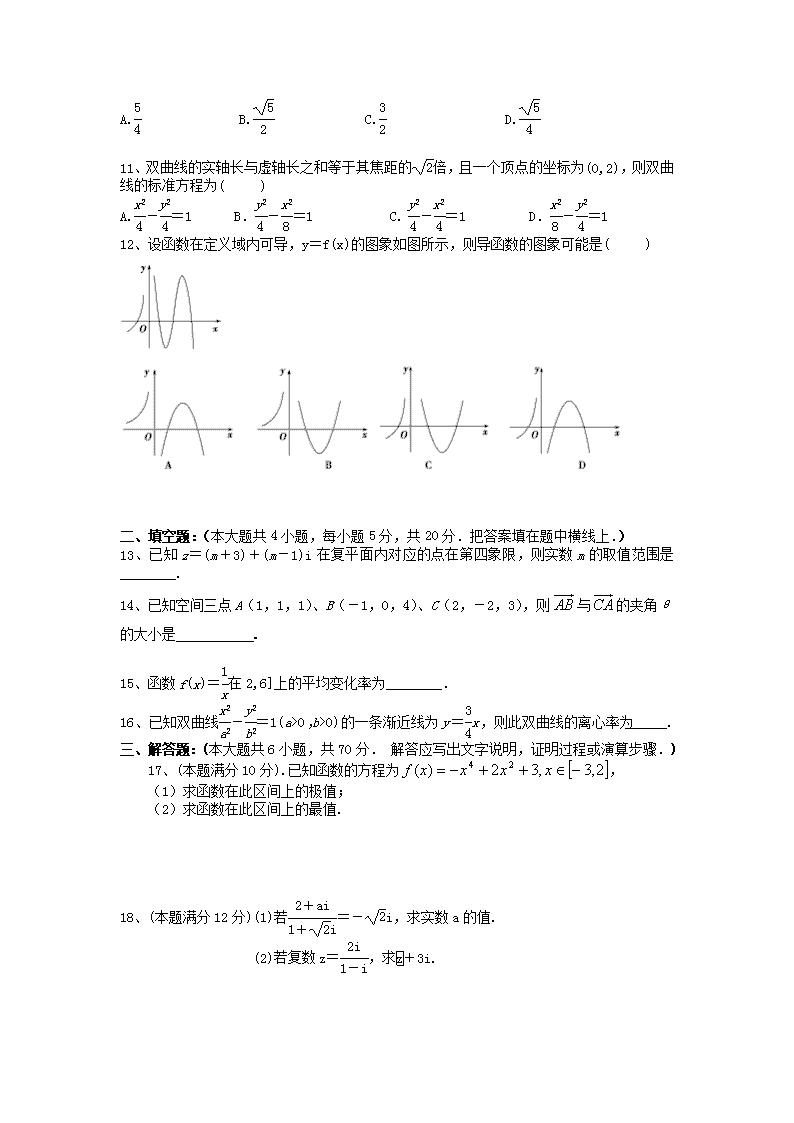
12、设函数在定义域内可导,y=f(x)的图象如图所示,则导函数的图象可能是( )
二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上.)
13、已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是________.
14、已知空间三点A(1,1,1)、B(-1,0,4)、C(2,-2,3),则与的夹角θ的大小是 .
15、函数f(x)=在2,6]上的平均变化率为________.
16、已知双曲线-=1(a>0,b>0)的一条渐近线为y=x,则此双曲线的离心率为______.
三、解答题:(本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤.)
17、(本题满分10分).已知函数的方程为,
(1)求函数在此区间上的极值;
(2)求函数在此区间上的最值.
18、(本题满分12分)(1)若=-i,求实数a的值.
(2)若复数z=,求+3i.
19、(本题满分12分)已知三棱锥中,,,,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
20、(本题满分12分)已知椭圆C的中心在坐标原点,焦点坐标为(2,0),短轴长为4.
(1)求椭圆C的标准方程及离心率;
(2)设P是椭圆C上一点,且点P与椭圆C的两个焦点F1、F2构成一个以∠PF2F1为直角的直角三角形,求的值.
21、(本题满分12分)已知曲线
(1) 求曲线在点处的切线方程;
(2) 求斜率为的曲线的切线方程。
22、(本题满分12分)如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为的直线与抛物线相交于A,B两点.
(1)用p表示|AB|;
(2)若·=-3,求这个抛物线的方程.
汪清六中期中考试高二理科数学试题答案
一、 选择题:
BCDAD CABDB CA
二、填空题:
13、-3<m<1; 14、 ; 15、- ; 16、
三、解答题:
17、解:(1)极大值4,极小值3 (2)最小值-60,最大值4
18、解:(1)依题意,得2+ai=-i(1+i)=2-i,
∴a=-,
(2)∵z==
=i(1+i)=-1+i,
∴=-1-i,
∴+3i=-1+2i.
20、解: (1)设椭圆C的标准方程为+=1.
由题意得c=2,b=2,∴a=4.
故椭圆C的标准方程为+=1,离心率e==.
(2)
∵∠PF2F1=90°.
∴|PF2|===3.
又∵|PF1|+|PF2|=2a=8,
∴|PF1|=5,∴=.
、
21、解:(1)因为在曲线上,且
所以,在处的切线的斜率为
所以曲线在处的切线方程为即
(2) 设切点的坐标为,则切线的斜率
所以
所以切点是或,
所以切线方程为或
即或
22、解: (1)抛物线的焦点为F,过点F且倾斜角为的直线方程为y=x-.
设A(x1,y1),B(x2,y2),由
得x2-3px+=0,
∴x1+x2=3p,x1x2=,
∴|AB|=x1+x2+p=4p.
(2)由 (1)知,x1x2=,x1+x2=3p,
∴y1y2==x1x2-(x1+x2)+=-+=-p2,∴·=x1x2+y1y2=-p2=-=-3,解得p2=4,∴p=2.