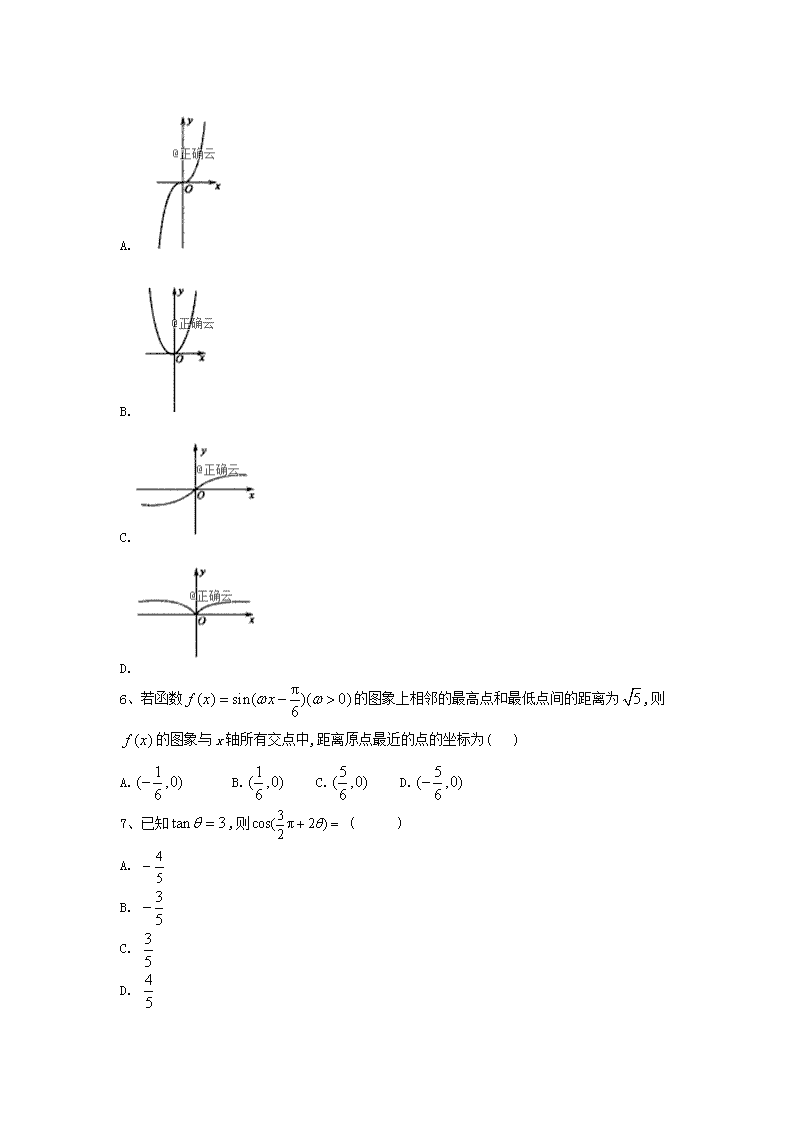2019届高考数学（理）倒计时模拟卷（2） 14页

‎2019高考数学（理）倒计时模拟卷（2）‎ ‎1、若全集,,则( ) A. B.‎ C. D.‎ ‎2、如图,在△中, ,若,则 (   )‎ A. B. C. D. ‎ ‎3、若为虚数单位，则( )‎ A. B. C.1 D.‎ ‎4、设两个变量x和y之间具有线性相关关系，它们的相关系数为r，y关于x的回归直线方程为，则（ ）‎ A. k与r的符号相同 B. b与r的符号相同 C. k与r的符号相反 D. b与r的符号相反 ‎5、函数的大致图像为(   )‎ A. B. C. D.‎ ‎6、若函数的图象上相邻的最高点和最低点间的距离为,则的图象与x轴所有交点中,距离原点最近的点的坐标为( ) A. B. C. D.‎ ‎7、已知,则 (   )‎ A. B. C. D. ‎ ‎8、已知数列的前n项和为,,数列满足,若对任意恒成立,则实数m的最小值为( ) A. B. C.或 D.‎ ‎9、已知是空间中两条不同的直线, 为空间中两个互相垂直的平面,则下列命题正确的是(   )‎ A.若,则 B.若,,则 C.若,,则 D.若,,则 ‎10、已知点P为双曲线右支上一点，分别为双曲线的左右焦点，点为的内心（三角形内切圆的圆心），若恒有成立，则双曲线的离心率取值范围为（ ）‎ A． B. C． D． ‎ ‎11、若关于x的方程在区间上有且只有一解,则正数的最大值是(   )‎ A.8          B.7          C.6          D.5‎ ‎12、已知,,若,则的最小值为(   )‎ A. B. C. D. ‎ ‎13、若展开式的二项式系数之和为,则展开式的常数项为__________‎ ‎14、在平面直角坐标系中,圆的方程为,若直线上至少存在一点,使得以该点为圆心, 为半径的圆与圆有公共点,则的最大值是                 .‎ ‎15、若整数满足不等式组，则的最小值为_________‎ ‎16、已知直线与圆相切且与抛物线交于不同的两点,则实数的取值范围是__________‎ ‎17、在中，内角的对边分别为，且 ‎1.若，的面积为，求；‎ ‎2.若，求角.‎ ‎18、在如图所示的几何体中,四边形是正方形, 平面,分别是线段,的中点, .‎ ‎1.求证: 平面;‎ ‎2.求平面与平面所成锐二面角的余弦值.‎ ‎19、《中华人民共和国民法总则》(以下简称《民法总则》)自年月日起施行。作为民法典的开篇之作,《民法总则》与每个人的一生息息相关.某地区为了调研本地区人们对该法律的了解情况,随机抽取人,他们的年龄都在区间上,年龄的频率分布及了解《民法总则》的人数如下表: ‎ 年龄 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 频数 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 了解《民法总则》 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎1. 填写下面列联表,并判断是否有的把握认为以岁为分界点对了解《民法总则》政策有差异; ‎ 年龄低于岁的人数 ‎ 年龄不低于岁的人数 ‎ 合计 ‎ 了解 ‎ ‎ ‎ ‎ ‎ 不了解 ‎ ‎ ‎ ‎ ‎ 合计 ‎ ‎2.若对年龄在的被调研人中各随机选取人进行深入调研,记选中的人中不了解《民法总则》的人数为,求随机变量的分布列和数学期望. ‎ 参考公式数据: ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎20、已知椭圆 : ()的两个焦点分别为,,离心率为,且过点.‎ ‎1.求椭圆 的标准方程;‎ ‎2. 、、、是椭圆上四个不同的点,两条都不与轴垂直的直线和分别过点,,且这两条直线互相垂直,求证: 为定值.‎ ‎21、已知函数 ‎1.当时,讨论 的极值情况;‎ ‎2.若,求的值.‎ ‎22、在平面直角坐标系中,直线的参数方程为 (为参数),以坐标原点为极点, 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,已知曲线的极坐标方程为,且直线经过曲线的左焦点.‎ ‎1.求直线的普通方程;‎ ‎2.设曲线的内接矩形的周长为,求的最大值.‎ ‎23、已知函数,.‎ ‎1.若恒成立,求的最小值;‎ ‎2.若,求不等式的解集.‎ 答案 ‎1.A 解析：∵全集,,∴.故选A.‎ ‎2.D 解析：由题意, ‎ ‎3.B ‎4.A ‎5.A ‎6.B 解析：由函数的图象上相邻的最高点和最低点间的距离为,设的最小正周期为T,可得,,所以,所以函数,令,得,,解得,,当时,,即是的一个离原点最近的点,故选B.‎ ‎7.C ‎8.A 解析：∵,∴,∴,由题意得,∴,.‎ 由,得,‎ ‎∴是数列的最大项.故选A.‎ ‎9.C 解析：由题设, ,则A选项,若,则,错误;‎ B选项,若,则错误;‎ D选项,若,当时不能得到,错误.‎ ‎10.B ‎11.B 解析：可变为,方程在区间上有且只有一解,即在区间上有且只有一个交点,如图,由已知可得:设函数的最小正周期为,则,,∴.‎ ‎12.D ‎13.20‎ ‎14.‎ 解析：由于圆的方程为,圆心为 由题意可知到的距离应不大于2,‎ 即.‎ 整理得,解得,‎ 故的最大值为.‎ ‎15.‎ ‎16.‎ 解析：因为直线与圆相切,所以,即 将直线方程代入抛物线方程并整理,得.‎ 由直线与抛物线相交于不同的两点,得 解得或 ‎17.‎ ‎1.‎ ‎2.或 ‎18.1.取中点,连接,‎ ‎∵分别是中点,‎ ‎∴,‎ ‎∵为中点,四边形为正方形,‎ ‎∴,‎ ‎∴,‎ 四边形为平行四边形,‎ ‎∴‎ ‎∵平面,平面,‎ ‎∴平面. 2.∵平面,且四边形是正方形,‎ 两两垂直,以为原点, 所在直线为轴,建立空间直角坐标系, 则 设平面法向量为,‎ 则, 即,‎ 取,‎ 设平面法向量为,‎ 则,即,‎ 取,‎ ‎∵.‎ ‎∴平面与平面所成锐二面角的余弦值为 ‎19答案:1.列联表：‎ 年龄低于岁的人数 年龄不低于岁的人数 合计 了解 不了解 合计 没有的把握认为以岁为分界点对了解《民法总则》政策有差异.‎ ‎2.的所有可能取值为 ‎ ‎ 则X的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ 所以的数学期望是 ‎20.1.∵,‎ ‎∴,‎ ‎∴,‎ ‎∴椭圆的方程为,‎ 又点在椭圆上,∴,‎ 解得,‎ ‎∴,‎ ‎∴椭圆的方程为. 2.由(1)得椭圆 的焦点坐标为,‎ 由已知,不妨设直线方程为.‎ 由直线与互相垂直,可得直线的方程为,‎ 由消去整理得,‎ 设,,‎ 则,‎ ‎∴,‎ 同理,‎ ‎∴,为定值.‎ ‎21.1. .‎ 因为,由得, 或.‎ ‎①当时, ,单调递增,故无极值.‎ ‎②当时, .,,的关系如下表:‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ 单调递增 极大值 单调递减 极小值 单调递增 故有极大值,极小值.‎ ‎③当时, .,,的关系如下表:‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ 单调递增 极大值 单调递减 极小值 单调递增 故有极大值,极小值.‎ 综上:当时, 有极大值,极小值;‎ 当时, 无极值;当时, 有极大值,极小值 2.令,则.‎ ‎(i)当时, ,所以当时, ,单调递减,‎ 所以,此时,不满足题意.‎ ‎(ii)由于与有相同的单调性,因此,由1知:‎ ‎①当时, 在上单调递增,又,‎ 所以当时, ;当时, .‎ 故当时,恒有,满足题意.‎ ‎②当时, 在单调递减,‎ 所以当时, ,‎ 此时,不满足题意.‎ ‎③当时, 在单调递减,‎ 所以当时, ,‎ 此时,不满足题意.综上所述: .‎ 解析：点睛:‎ 本题考查了导数的综合运用,在求函数的极值时,分类讨论了不同参量情况下的取值问题,在解答不等式的问题中,采用换元法,分类讨论各种情形的结果,同时也考查了学生的计算能力及分类讨论,属于难题.‎ ‎22.1. 2. ‎ 解析：1.因为曲线的极坐标方程为,‎ 即.‎ 将,代入上式,‎ 得即 所以曲线的直角坐标方程为.‎ 于是所以 由消去参数,得直线l的普通方程为.‎ 将代入直线方程得.‎ 所以直线的普通方程为. 2.设椭圆的内接矩形在第一象限的顶点为 所以椭圆的内接矩形的周长为 (其中),‎ 故椭圆的内接矩形的周长的最大值.‎ ‎23.1. ‎ ‎,的最小值为 2.①当时, ,得,‎ ‎②当时, ,得,‎ ‎③当时, ,得,‎ 综上,不等式解集为 ‎