2018届二轮复习空间几何体：第5节几何体的体积学案（全国通用） 9页

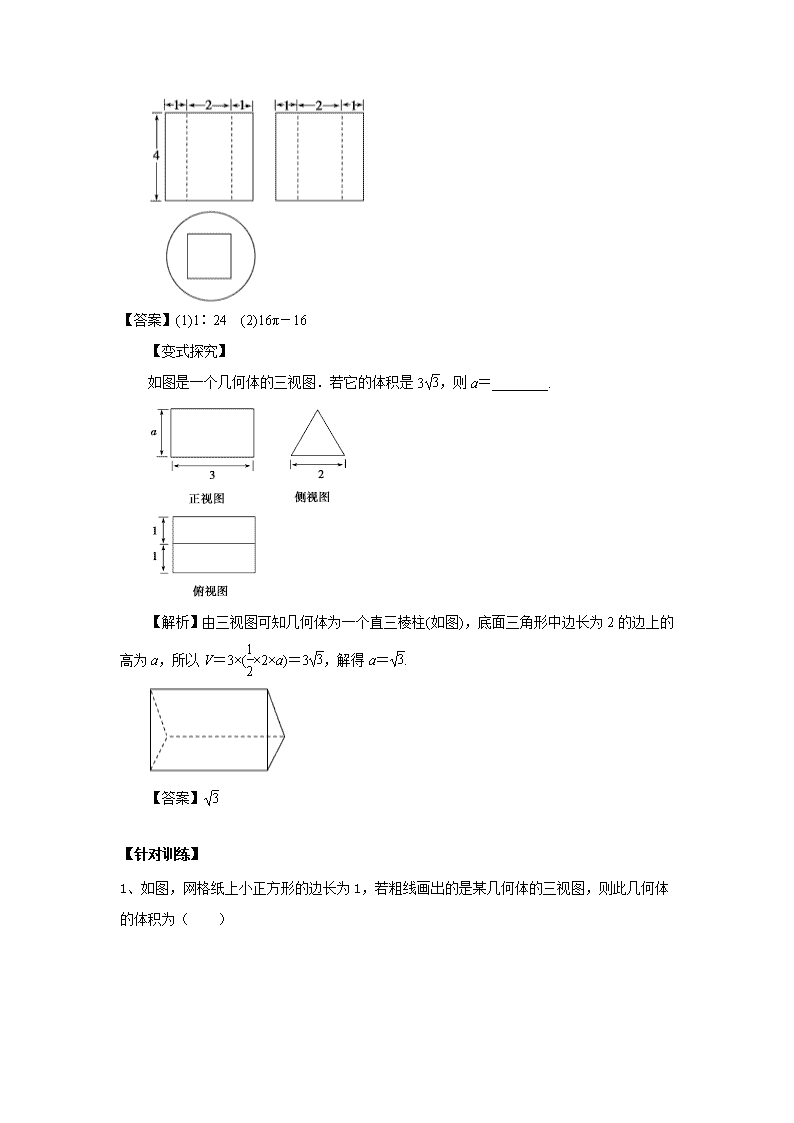
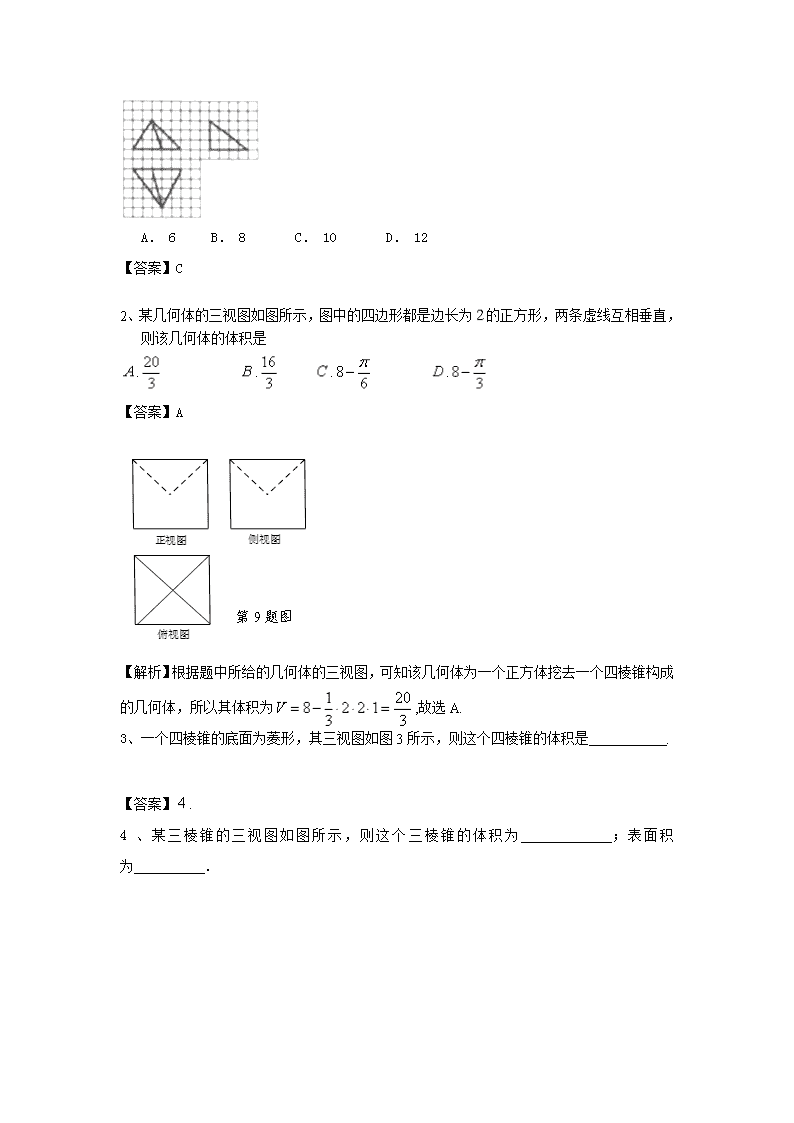
第5节 几何体的体积 ‎【基础知识】‎ 圆柱的体积 ‎ 圆锥的体积 ‎ 圆台的体积 ‎ 球体的体积 ‎ ‎ 正方体的体积 ‎ ‎ 正方体的体积 ‎ ‎【规律技巧】‎ 求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；‎ ‎ 若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．‎ ‎【典例讲解】‎ 例1、(1)如图，在三棱柱A1B1C1－ABC中，D，E，F分别是AB，AC，AA1的中点．设三棱锥F－ADE的体积为V1，三棱柱A1B1C1－ABC的体积为V2，则V1∶V2＝________.‎ ‎(2)某几何体的三视图如图所示，则该几何体的体积是________．‎ ‎【答案】(1)1∶24　(2)16π－16‎ ‎【变式探究】‎ 如图是一个几何体的三视图．若它的体积是3，则a＝________.‎ ‎【解析】由三视图可知几何体为一个直三棱柱(如图)，底面三角形中边长为2的边上的高为a，所以V＝3×(×2×a)＝3，解得a＝.‎ ‎【答案】 ‎【针对训练】‎ ‎1、如图，网格纸上小正方形的边长为1，若粗线画出的是某几何体的三视图，则此几何体的体积为（　　）‎ ‎　 A． 6 B． 8 C． 10 D． 12‎ ‎【答案】C ‎2、某几何体的三视图如图所示，图中的四边形都是边长为的正方形，两条虚线互相垂直，则该几何体的体积是 ‎. . . .‎ ‎【答案】A ‎【解析】根据题中所给的几何体的三视图，可知该几何体为一个正方体挖去一个四棱锥构成的几何体，所以其体积为,故选A.‎ ‎3、一个四棱锥的底面为菱形，其三视图如图3所示，则这个四棱锥的体积是 .‎ ‎【答案】.‎ ‎4、某三棱锥的三视图如图所示，则这个三棱锥的体积为 ；表面积为 ． ‎ ‎1‎ 正视图 侧视图 俯视图 ‎1‎ ‎1‎ ‎1‎ ‎【答案】；．‎ ‎5、一个几何体的三视图如图所示（单位：），一个几何体的三视图如图所示（单位：），则该几何体的体积为 .‎ ‎【答案】‎ ‎【解析】由三视图可得该几何体为圆柱与圆锥的组合体，其体积.‎ ‎6、已知某几何体的三视图如右图所示，正视图和侧视图是边长为1的正方形，俯视图是腰长为1的等腰直角三角形，则该几何体的体积是（ ）．‎ ‎（A） （B） （C） （D）‎ ‎【答案】C ‎【解析】由三视图可知该几何体为直三棱柱，故体为，故选C．‎ ‎7、已知一个空间几何体的三视图如右图所示，根据图中 标出的尺寸（单位：cm），可得这个几何体的体积是（　　）‎ A．4 cm B．5 cm3 C．6 cm3 D．7 cm3‎ ‎【答案】A ‎【解析】几何体为一个四棱锥：高为2，底面为直角梯形，上底为2，下底为4，高为2，因此体积为，选A.‎ ‎8、一个简单几何体的正视图、侧视图如右图所示，则其俯视图不可能为（ ）‎ ‎①长方形；②正方形；③圆；④椭圆.‎ 中的 A.①② B.②③ ‎ C.③④ D.①④ ‎ ‎【答案】B ‎【解析】若俯视图为正方形，则正视图中的边长3不成立；若俯视图为圆，则正视图中的边长3也不成立.‎ ‎9、一个几何体的三视图如图所示，则该几何体的体积是 ‎ A． B．1 C． D．‎ ‎【答案】.‎ ‎10、某几何体的三视图如图所示，则该几何体的体积为( )‎ A. B. C. D. ‎【答案】C ‎【练习巩固】‎ ‎1、某几何体的三视图如图所示，则该几何体的体积为 A、 B、‎ C、 D、‎ ‎【答案】A ‎【解析】这是一个三棱锥与半个圆柱的组合体，，选A.‎ ‎2、在梯形中，， .将梯形绕所在的直线旋转一周而形成的曲面所围成的几何体的体积为（ ）‎ ‎（A） （B） （C） （D） ‎ ‎【答案】C ‎3、某几何体的三视图如图所示（单位：cm），则该几何体的体积是（ ）‎ ‎ A. B. C. D. ‎ ‎【答案】C.‎ ‎【解析】由题意得，该几何体为一立方体与四棱锥的组合，如下图所示，∴体积 ‎，‎ 故选C.‎ ‎4．(2013年高考重庆卷)某几何体的三视图如图所示，则该几何体的体积为(　　)‎ A.　　　B.　　　C．200　　　D．240‎ 解析：由三视图可得该几何体是上、下底面均为矩形，左、右侧面均为等腰梯形的多面体，如图所示，故体积V＝×(2＋8)×4×10＝200.‎ 答案：C ‎5.(2013年高考广东卷)某四棱台的三视图如图所示，则该四棱台的体积是(　　)‎ A．4　　　　　 B. C.　　　　　 D．6‎ ‎6.(2013年高考全国新课标卷Ⅰ)某几何体的三视图如图所示，则该几何体的体积为(　　)‎ A．16＋8π B．8＋8π ‎ C．16＋16π D．8＋16π