2017-2018学年湖南省双峰县第一中学高二上学期第二次月考数学（文）试题 8页

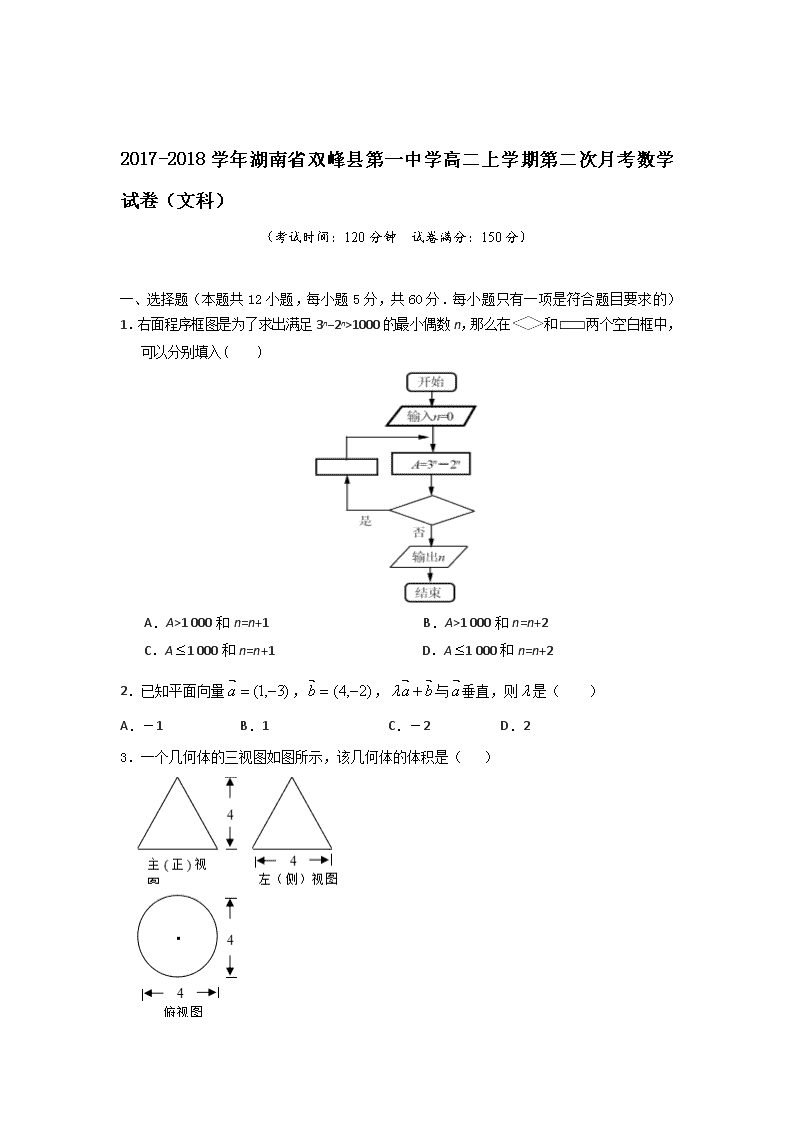
2017-2018 学年湖南省双峰县第一中学高二上学期第二次月考数学 试卷（文科） （考试时间：120 分钟 试卷满分：150 分） 一、选择题（本题共 12 小题，每小题 5 分，共 60 分．每小题只有一项是符合题目要求的） 1．右面程序框图是为了求出满足 3n−2n>1000 的最小偶数 n，那么在 和 两个空白框中， 可以分别填入(　　) A．A>1 000 和 n=n+1 B．A>1 000 和 n=n+2 C．A 1 000 和 n=n+1 D．A 1 000 和 n=n+2 2．已知平面向量 ， ， 与 垂直，则 是（ ） A．－1 B．1 C．－2 D．2 3．一个几何体的三视图如图所示，该几何体的体积是（ ） ≤≤ )3,1( −=a )2,4( −=b ba +λ a λ A． B． C． π D． 4．若 的内角 A，B，C 的对边 为满足 则角 A 的大小为(　　) A. B. C. D. 5. 已知在△ABC 中，三个内角 A，B，C 的对边分别为 a，b，c，若△ABC 的面积为 S，且 2S＝(a＋b)2－c2，则 tanC 等于(　　) A． B． C．－ D． － 6．等差数列 的前 项和为 ，已知 ，则 的值为（ ） A. 38 B. -19 C. -38 D. 19 7 ． 已 知 数 列 满 足 ， 且 ， 则 的值是(　 ) A．－ B． C．5 D． 8.已知等差数列 满足, =3, =－ 则数列 的前 10 项和为（ ） A．15 B．75 C．45 D．60 9、设变量 满足 则 的最大值和最小值分别为（ ） A、 B、 C、 D、 10．若不等式 对任意正实数 x，y 恒成立，则实数 的取值范围是（ ） A． B． C． D． 11．下列命题中为真命题的是（ ） A．命题“若 ，则 ”的否命题 B．命题“若 ，则 ”的逆命题 C．命题“若 ，则 ”的否命题 ΔABC a b c， ， 2 2 2a b c bc= + − ， π 6 π 3 2π 3 5π 6 3 4 4 3 4 3 3 4 { }na n nS 1 5 10 15 19 2a a a a a− − − + = 19S { }na * 3 1 3log 1 l g ( )on na a n+ = + ∈N 2 4 6 9a a a+ + = 1 5 7 9 3 lo (g )a a a+ + 5− yx,    ≥ ≤− ≤+ 0 1 1 x yx yx yx 2+ 1,1 − 2,2 − 2-1， 1-2， ( ) 1 4x y mx y  + + ≥   m [ )3,+∞ [ )6,+∞ ( ],9−∞ ( ],12−∞ 3 16 3 16 5 1 5 1 }{ na 5a 7a 3 { }na 1>x 12 >x yx > || yx > 1=x 022 =−+ xx D．命题“若 ，则 ”的逆否命题 12．△ABC 的内角 A、B、C 的对边分别为 a、b、c，则“a>b”是 “ < ”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 二、填空题（本题共 4 小题，每小题 5 分，共 20 分） 13.如图，已知 ， ， ， ，则 __________. 14．直线 被圆 截得的弦长为__________. 15．对于数列 ，定义其积数是 ,若数列 的积数是 ，则 =__________. 16． 给出下列四个命题： ①． 中， 是 成立的充要条件； ②．当 时，有 ； ③．已知 是等差数列 的前 n 项和，若 ，则 ； ④．若函数 为 R 上的奇函数，则函数 的图象一定关于点 成 中心对称． 其中所有正确命题的序号为 ． 三、解答题（本大题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分 10 分）已知函数 45CAB∠ = ° 15ACB∠ = ° 6AC = 7CD = BD = D C A B { }na ( )1 2 3 ,n n a a a aV n Nn + ⋅ ⋅ ⋅⋅⋅⋅⋅⋅= ∈ { }na 1nV n= + na ABC∆ A B> sin sinA B> 0 1x x> ≠且 1ln 2lnx x + ≥ { }na 7 5S S> 9 3S S> 2( ) sin 2 3(1 2sin ) 1f x x x= − − − + 3tan =x 3 π=x A2cos B2cos 043 =−− yx ( ) 42 22 =+− yx nS )2 3( −= xfy )(xfy = )0,2 3(F （1）求 的最小正周期及其单调减区间； （2）当 时，求 的值域. 18．（本小题满分 12 分）(1)设集合 和 ，从集合 中随机取一 个数作为 ，从 中随机取一个数作为 .求所取的两数中能使 时的概率； (2)设点 是区域 内的随机点，求能使 时的概率. 19.（本小题满分 12 分）如图，矩形 中， 平面 ， ， 为 上的点，且 平面 . （1）求证： 平面 ； （2）求证： 平面 . 20．（本小题满分 12 分）设 是公比大于 1 的等比数列， 为数列 的前 项和．已 知 ，且 构成等差数列． （Ⅰ）求数列 的通项公式； （Ⅱ）令 ,求数列 的前 项和 ． ( )f x [ , ]6 6x π π∈ − ( )f x ABCD AD ⊥ ABE 2AE EB BC= = = F CE BF ⊥ ACE AE ⊥ BCE / /AE BFD { }na nS { }na n 3 7S = 1 2 33,3 , 4a a a+ + { }na n nb na= { }nb n nT    > > ≤−+ 0 0 06 y x yx 21．（本小题满分 12 分）已知函数 ，其中 m 是实数 (1)若函数 有零点，求 m 的取值范围； (2)设不等式 的解集为 A，若 ，求 m 的取值范围. 22．（本小题满分 12 分）已知 ． （Ⅰ）求函数 的定义域； （Ⅱ）证明函数 为奇函数； （Ⅲ）求使 ＞0 成立的 x 的取值范围． mxmmxxf +−−= )1()( 2 )(xf mmxxf +<)( )3,(−∞⊆A 文科数学 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D A C B C C B B B C B C 二、填空题 13、 3 14、 15、 16、 ①③ 三、解答题 17、（1）最小正周期为π，单调减区间为 ， （2）值域为[-1，1] 18、（1） （2） 19、（1）、证明：∵ 平面 ， ，∴ 平面 ，则 又 平面 ，则 ,又 ,∴ （2）、由题意可得 是 的中点，连接 平面 ，则 ，而 ， 是 中点,在 中， ， 平面 2 1 1 na n n = +  − ( ) ( ) 1 2, n n n N+ = ≥ ∈ AD ⊥ ABE / /AD BC BC ⊥ ABE AE BC⊥ BF ⊥ ACE G AC FG BF ⊥ ACE CE BF⊥ BC BE= F∴ EC AEC∆ / /FG AE / /AE∴ BFD 32 3 1=p BFAE ⊥ BBFBC = BCEAE 平面⊥ 20、（1）数列 的通项为 （2） 21、（1）当 m=0 时，f(x)=-x,零点为 x=0,当 m≠0 时，f(x)为二次函数，由∆≥0 得(1-m)2-4m2 ≥0 即 3m2+2m-1≤0 解得-1≤m≤ 且 m≠0 综上所述可知函数有零点，则-1≤m≤ （2）当 m=0 时，解得 x>0,显然 A ⊆（-∞，3）不成立， 当 m>0 时，不等式可化为 ，解得 ，若 A ⊆（-∞，3）则 ，即 m≥ 当 m<0 时，不等式可化为 ，解得 ，显然 A ⊆（-∞，3）不 成立. 综上所述,有 m≥ 22、（1）函数 的定义域为 （2）定义域为（－1，1）关于原点对称， ∴ ． ∴函数 为奇函数． （3）当 a>1 时， ， 当 时， ， { }na 12n na −= ( )1 2 1n nT n∴ = − ⋅ + 3 1 3 1 012 <− xmx mx 10 << 31 ≤ m 3 1 012 >− xmx 01 >< xmx 或 3 1 ( )1,1− 10 << x 10 << a 01 <<− x