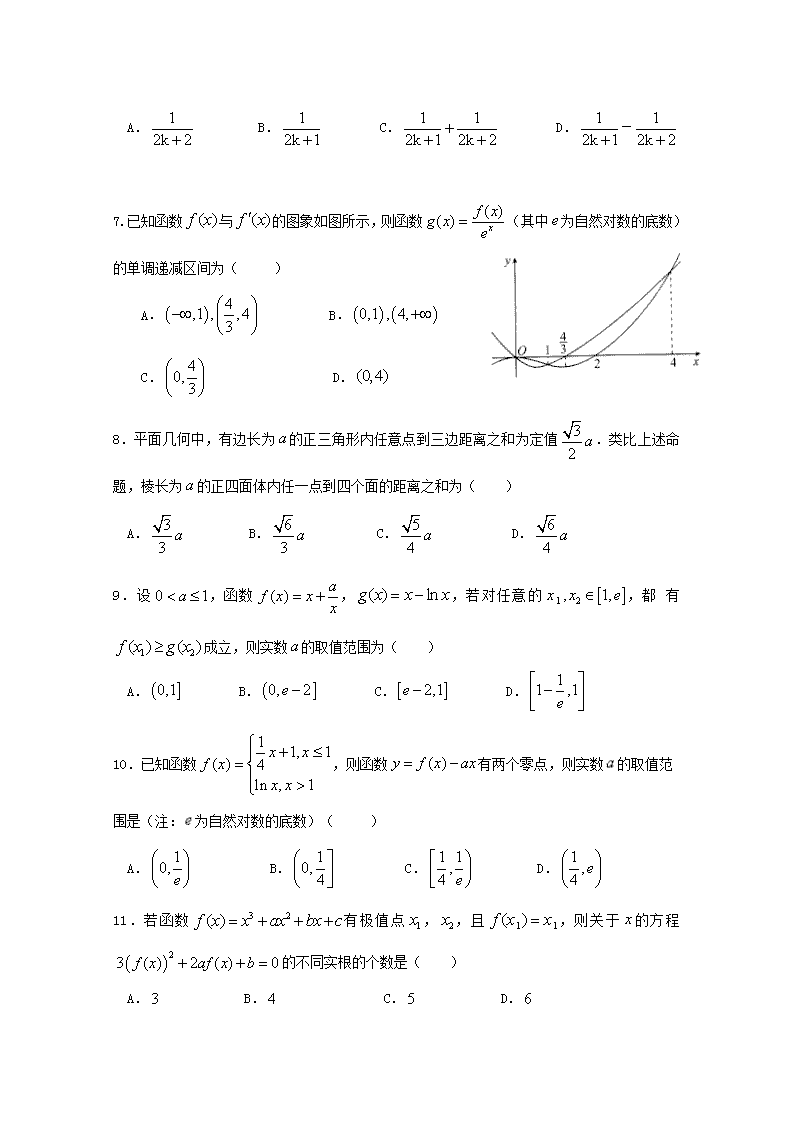2018-2019学年福建省福州市八县（市）一中高二下学期期中联考数学（理）试题 Word版 11页

福建省福州市2018-2019学年第二学期八县（市）一中期中联考 高中 二 年 数学（理） 科试卷 ‎ 完卷时间：120分钟 满分：150分 一、选择题（本大题12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求．）‎ ‎1．用反证法证明命题“三角形三个内角至少有一个不大于”时题应假设（  ）‎ A． ‎ 三个内角都不大于 B． 三个内角都大于 C． 三个内角至多有一个大于 D．三个内角至多有两个大于 2． 复数满足，则的虚部是（  ） ‎ A． B． C． D． ‎ ‎3．将曲线按变换后的曲线的参数方程为（ ）‎ A． B． C． D．‎ ‎4．设，，，则的大小关系( )‎ A．a>b>c B．a>c>b C．b>a>c D．b>c>a ‎5．已知函数的导函数为，且满足，则(　 )‎ A． B． C． D．‎ ‎6．数学归纳法证明，过程中由到时，左边增加的代数式为（ ）‎ A． B． C． D．‎ ‎7.已知函数与的图象如图所示，则函数（其中为自然对数的底数）的单调递减区间为（ ）‎ ‎ A． B． ‎ ‎ C． D． ‎ ‎8．平面几何中，有边长为的正三角形内任意点到三边距离之和为定值．类比上述命题，棱长为的正四面体内任一点到四个面的距离之和为（ ）‎ A． B． C． D．‎ ‎9．设，函数，，若对任意的，都 有成立，则实数的取值范围为（ ）‎ A． B． C． D．‎ ‎10．已知函数，则函数有两个零点，则实数的取值范围是（注：为自然对数的底数）（ ）‎ A． B． C． D．‎ ‎11．若函数有极值点，，且，则关于的方程的不同实根的个数是（ ）‎ A． B． C． D．‎ ‎12．已知函数的定义域是，是的导数，，对，有是自然对数的底数）．不等式的解集是（ ）‎ A． B． C． D．‎ 二、填空题（本大题共4小题，每小题5分，共20分.）‎ ‎13．若且，那么的最小值为________ ． ‎ ‎14．已知函数在定义域内存在单调递减区间，则实数的取值范围是________ ．‎ ‎15．我国古代数学名著《九章算术》中割圆术记载：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”其体现的是一种无限与有限的转化过程，比如在中，“…”即代表无限次重复，但原式却是个定值，这可以通过方程确定，则________ ． ‎ ‎16． 对于定义在上的函数，若存在距离为的两条直线和，使得对任意都有恒成立，则称函数有一个宽度为的通道．给出下列函数： ‎ ‎①； ②； ③； ④．‎ 其中在区间上有一个通道宽度为的函数是 （写出所有正确的序号）．‎ 三、解答题（本大题6小题，共70分. 解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（10分）在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为，过点的直线的参数方程为（为参数），直线与曲线交于两点．‎ ‎（1）写出曲线的直角坐标方程和直线的普通方程；‎ ‎（2）若成等比数列，求的值． ‎ ‎18．（12分）已知二次函数的图象与直线相切于点．‎ ‎（1）求函数的解析式；‎ ‎（2）求由曲线与直线，所围成的封闭图形的面积．‎ ‎19．（ 12分）设为虚数单位，．‎ 已知， ‎ ‎，‎ ‎ ．‎ ‎（1）你能得到什么一般性的猜想？请用数学归纳法证明猜想；‎ ‎（2）已知，试利用（1）的结论求． ‎ ‎20．（12分）某厂生产某种电子元件，如果生产出一件正品，可获利元，如果生产出一件次品，则损失元．已知该厂制造电子元件过程中，次品率与日产量的函数关系是：． ‎ ‎(1)写出该厂的日盈利额(元)用日产量(件)表示的函数关系式；‎ ‎(2)为获最大日盈利，该厂的日产量应定为多少件？‎ ‎21．（12分）已知函数．‎ ‎（1）求的极值；‎ ‎（2）设若对，求的取值范围．‎ ‎22．（12分）已知；‎ ‎（1）当时，求的单调区间；‎ ‎（2）求证：当时，方程在上无解．‎ ‎2018-2019学年第一学期八县（市）一中期中联考 高二数学(理科)参考答案 一、选择题（每小题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B A D C A D B B C C A D 二、填空题（每小题5分，共20分）‎ ‎13． 14． 15． 16．①③④‎ 三、解答题（本大题共6小题，共70分，解答应写出文字说明,证明过程或演算步骤）‎ ‎17．解：(1)曲线C的极坐标方程为，‎ 等式两边同乘，得①. ……………………1分 ‎ ‎ 将 代入①中，‎ 得曲线C的直角坐标方程为． ……………………2分 将直线的参数方程消去，得直线的普通方程为 …………4分 ‎ (2)将直线的参数方程代入曲线C的直角坐标方程)中，‎ 得 ……………………5分 由且，得 ……………………6分 设两点对应的参数分别为，‎ 则有， ‎ ‎∴同正． ……………………7分 ‎∵ 成等比数列∴‎ 又∵ ，‎ ‎∴， 即( ……………………8分 ‎∴， ‎ ‎ 解得（舍去）或 满足 ‎∴的值为． ……………………10分 ‎18．解：（1） ……………………1分 当时，， 即切点 …………………2分 ‎∴即解得 …………………5分 ‎∴ …………………6分 ‎（2）的图象，直线及直线所围成的封闭区域如图所示 面积 …………9分 ‎ ………12分 ‎ ‎ ‎19．解（1）猜想（）成立 ………1分 证明：①当n=1时，左边=右边=所以猜想成立 ………………2分 ‎ ②假设当时，猜想成立，‎ 即 ……………………………3分 则当时，‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 当 时，猜想也成立 …………………………5分 综上，由① ②可得对任意，猜想成立 …………………………6分 ‎(2) …………………8分 ‎ ………………………9分 ‎ ………………………10分 ‎ ……………………… 11分 ‎ …………………………12分 ‎20．解：(1)由意可知，每天生产件，次品数为，正品数为 …………1分 因为次品率，当每天生产件时，‎ 有件次品，有件正品． …………………2分 所以 ‎ ………………………5分 ‎(2) ………………………7分 由得或 (舍去)． ………………………8分 当0