数学文卷·2018届广西桂林市第一中学高二下学期期中质量检测（2017-04） 7页

‎┄┄┄密┄┄┄封┄┄┄装┄┄┄订┄┄┄线┄┄┄内┄┄┄不┄┄┄要┄┄┄答┄┄┄题┄┄┄‎ 年级: 班级： 　班 姓名： ‎ 高 初 本人愿意在考试中 自觉遵守学校考场规则。‎ ‎⊙‎ ‎⊙‎ 桂林市第一中学2016～2017学年度下学期期中质量检测试卷 ‎ 高二数学（文科）‎ ‎（用时120分钟，满分150分）‎ 注意事项： 1．试卷分为试题卷和答题卡两部分，在本试题卷上作答无效；‎ ‎2．考试结束后，只将答题卡交回，试题卷不用交，自己保管好以备讲评使用．‎ ‎ ‎ 第Ⅰ卷 ‎ 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1．设集合 ，，则 （　　）‎ ‎ A． B． C． D.‎ ‎2．设复数满足,则（　　）‎ ‎ A． B． C． D．‎ ‎3．若大前提是：任何实数的平方都大于0，小前提是： ，结论是： ，那么这个演绎推理出错在（　　）‎ A．大前提出错 B．小前提出错 C．推理过程出错 D．没有出错 ‎4．在复平面内,复数(为虚数单位)的共轭复数对应的点位于（　　）‎ ‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎5．已知，则（ ）‎ A． B． C． D． ‎ ‎6．函数的定义域是（ ）‎ A．[-1，3) B．(-∞，-1] C．[3，+∞） D．(3,+∞) ‎ ‎7．函数的零点所在区间是 （ ）‎ ‎ A．(1,2) B．(0,1) C．(-1,0) D．(-2,-1) ‎ ‎8．函数在[0，3]上的最大值和最小值分别是（ ）‎ A．12，-15 B．5，-4 C．5，-15 D．12，-4‎ ‎9．曲线在点处的切线方程为( )‎ ‎ A． B． C． D．‎ ‎10．如图给出的是计算的值 的一个程序框图，其中判断框内应填入的条件是（ ）‎ A．i>10 B．i<10 C．i<20 D．i>20‎ ‎11．若函数f(x)＝kx－ln x在区间(1，＋∞)单调递增，则 k的范围是(　　)‎ ‎ A．(－∞，－2] B．(－∞，－1] ‎ C．[1，＋∞) D．[2，＋∞)‎ ‎12．点在曲线上，为曲线在点处的切线的倾斜角，则的取值范围是（　　）‎ ‎ A．[0,) B． C． D．‎ 第Ⅱ卷 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．已知 ．‎ ‎14．已知函数，则 ．‎ ‎15．设, 若,则=_________． ‎ ‎16．对于函数， 给出下列四个命题：‎ ‎① 存在，使；②函数f(x)的图象关于直线对称；‎ ‎③存在，使函数的图象关于坐标原点成中心对称； ‎ ‎④函数f(x)的图象向左平移就能得到的图象．‎ 其中正确命题的序号是 ．‎ 三、解答题（本大题共6小题，共70分．解答应给出文字说明、证明过程或演算步骤．）‎ ‎17．（本题满分10分）(1)已知， i是虚数单位 ，若，求；‎ ‎(2)设，是纯虚数，其中i是虚数单位, 求。‎ ‎18．（本题满分12分）在中，内角A, B, C所对的边分别是a, b, c，若，，‎ ‎，求边a及角B、C的值。‎ ‎19．（本题满分12分）已知函数。‎ ‎（1）求函数的单调区间； （2）求函数的极值. 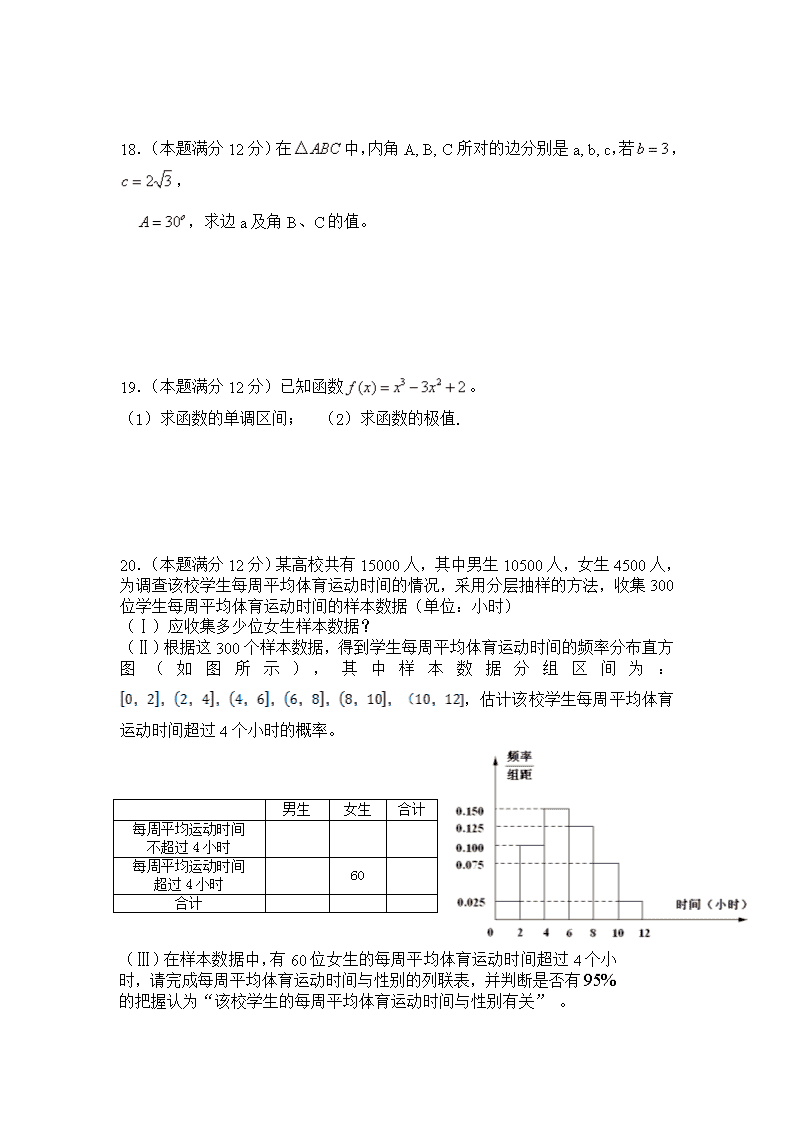‎ ‎20．（本题满分12分）某高校共有15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）‎ ‎（Ⅰ）应收集多少位女生样本数据？‎ ‎（Ⅱ）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据分组区间为：，估计该校学生每周平均体育运动时间超过4个小时的概率。‎ 男生 女生 合计 每周平均运动时间 不超过4小时 每周平均运动时间 超过4小时 ‎60‎ 合计 ‎（Ⅲ）在样本数据中，有60位女生的每周平均体育运动时间超过4个小时，请完成每周平均体育运动时间与性别的列联表，并判断是否有的把握认为“该校学生的每周平均体育运动时间与性别有关” 。 ‎ 附： ‎ ‎ ‎ ‎0.10‎ ‎0.05‎ ‎0.010‎ ‎0.005‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎7.879‎ ‎21．（本题满分12分）在△ABC中,内角A,B,C的对边分别是a,b,c,且a2=b2+c2+bc.‎ ‎(1)求A； (2)设a=,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值。‎ ‎22．（本题满分12分）已知函数。‎ ‎（1）若f(x)在[1,+∞）上是增函数，求实数a的取值范围；‎ ‎（2）若函数至多有两个零点，求实数a的取值范围。‎ ‎2016-2017学年度下学期段考高二文科数学答案 一、选择题 ‎1、D  2、B  3、A  4、D  5、C ‎ ‎6、D  7、C  8、C  9、B  10、A  ‎ ‎11、C  12、D 二、填空题 ‎13、-3/4 14、2 15、-1 16、②③‎ 三、解答题 ‎17、解：（1）因为（a+i）（1+i）=bi， 所以a-1+（a+1）i=bi，…………3分 由复数相等，知：a−1＝0 a+1＝b 解得：a=1, b=2. ………………5分 ‎ （2）（一个条件2分，结论一分）‎ ‎18、解：依题意知 a2=b2+c2-2bccos30°=9+12-2Í3ÍÍcos30°=21-18=3‎ ‎ ∴ a=‎ ‎∵ a=，b=3，A=30°‎ ‎ ∴ ∴ sinB= 即：B=60°或者B=120°‎ ‎ ∴ 当B=60°时，C=90°； 当B=120°时，C=30°。‎ ‎19、解：（1）由f（x）=x3-3x2+2，所以f′（x）=3x2-6x=3x（x-2）. ………2分 由f′（x）＞0知：x＜0或x＞2时； ‎ 由f′（x）＜0知：0＜x＜2时。 …………5分 所以，函数f（x）的单调递增区间是（-∞，0），（2，+∞）．单调递减区间是（0，2）． …………6分 ‎（2）＝3x2-6x．令=0，解得x=2或x=0， ……………7分 当x变化时，，的变化情况如下表： ……………10分 x ‎（-∞，0）‎ ‎0‎ ‎（0,1）‎ ‎2‎ ‎（1，+∞）‎ ‎+‎ ‎0‎ ‎-‎ ‎0‎ ‎+‎ ‎↑‎ ‎2‎ ‎↓‎ ‎-2‎ ‎↑‎ 因此，当x=2时，有极小值，且   当x=0时， 有极大值，且 ……………12分 ‎20、解：（1）90； ……3分 （2）0.75； ……6分 ‎（3）K2=4.762，有95%把握认为相关。……12分（4+2）‎ ‎21、解：（1）A=150°；……5分（2）最大值为3，此时B=15°；……12分 ‎22、解：（1）; ……6分 （2）. ……6分