- 316.00 KB
- 2024-02-03 发布
应 县 一 中 高 二 年 级 月 考 一
数 学 试 题(理) 2018.9
时间:120分钟 满分:150分 命题人:于文君
一.选择题(共12题,每题5分)
1.若直线与直线所成的角相等,则的位置关系为( )
A.相交 B.平行 C.异面 D.以上答案都有可能
2.下列说法中正确的是( )
A.棱柱的侧面可以是三角形
B.正方体和长方体都是特殊的四棱柱
C.所有的几何体的表面都能展成平面图形
D.棱柱的各条棱都相等
3.给定下列命题,其中正确命题为( )
A.若一直线与一个平面不平行,则此直线与平面内所有直线不平行,
B.若一直线平行于一个平面,则此直线平行于平面内所有直线;
C.若一直线与一个平面不垂直,则此直线与平面内所有直线不垂直;
D.若一直线垂直于一个平面,则此直线垂直于平面内所有直线;
4.如图,在三棱锥A﹣BCD中,AC⊥AB,BC⊥BD,平面ABC⊥平面BCD.
①AC⊥CD②AD⊥BC③平面ABC⊥平面ABD④平面ACD⊥平面ABD.
以上结论正确的个数有( )
A.1 B.2
C.4 D.5
5.,为异面直线, 平面,平面,直线满足,,,,则( )
A. 且 B. 且
C. 与相交,且交线垂直于 D. 与相交,且交线平行于
6.已知A(5,2),B(﹣1,4),则AB的垂直平分线方程为( )
A.x﹣3y+7=0 B.3x﹣y﹣3=0 C.3x+y﹣7=0 D.3x﹣y﹣7=0
7.下列说法中正确的是( )
A.平行的两条直线的斜率相等
B.只有斜率相等的两条直线才平行
C.平行的两条直线的倾斜角一定相等
D.垂直的两直线的斜率之积为-1
8.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A.2 B.4 C.6 D.8
9.过点(2,3),且到原点的距离最大的直线方程是( )
A.3x+2y﹣12=0 B.2x+3y﹣13=0 C.x=2 D.x+y﹣5=0
10.一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面( )
A.至多有一个是直角三角形 B.至多有两个是直角三角形
C.可能都是直角三角形 D.必然都是非直角三角形
11.在正方体ABCD﹣A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,当点Q在( )位置时,平面D1BQ∥平面PAO.
A.Q与C重合 B.Q与C1重合
C.Q为CC1的三等分点 D.Q为CC1的中点
12.棱长为4的正方体ABCD—A1B1C1D1中,P、Q是上两动点,且PQ=1,则三棱锥P—AQD的体积为( )
A. 8 B. C. 3 D.
二.填空题(共4题,每题5分)
13.两个不重合的平面可以把空间分成__________部分.
14.已知直线m,n与平面α,β,若m∥α,n∥β且α∥β,则直线m,n的位置关系为 .
15.已知M(﹣2,1),N(3,2),直线y=kx+1与线段MN有交点,则k的范围是 .
16.将正方形沿对角线折成直二面角,有如下四个结论:
①;②是等边三角形;③与平面成的角;④与所成的角为。其中正确的编号是 .
三.解答题(共6题,第17题为10分,其余各题每题为12分)
17.在空间四边形中,、、、分别是边、、、的中点,对角线且它们所成的角为。
( 1 )求证:,( 2 )求四边形的面积。
18.过点引三条长度相等不共面的线段、、,且,
,求证:平面平面。
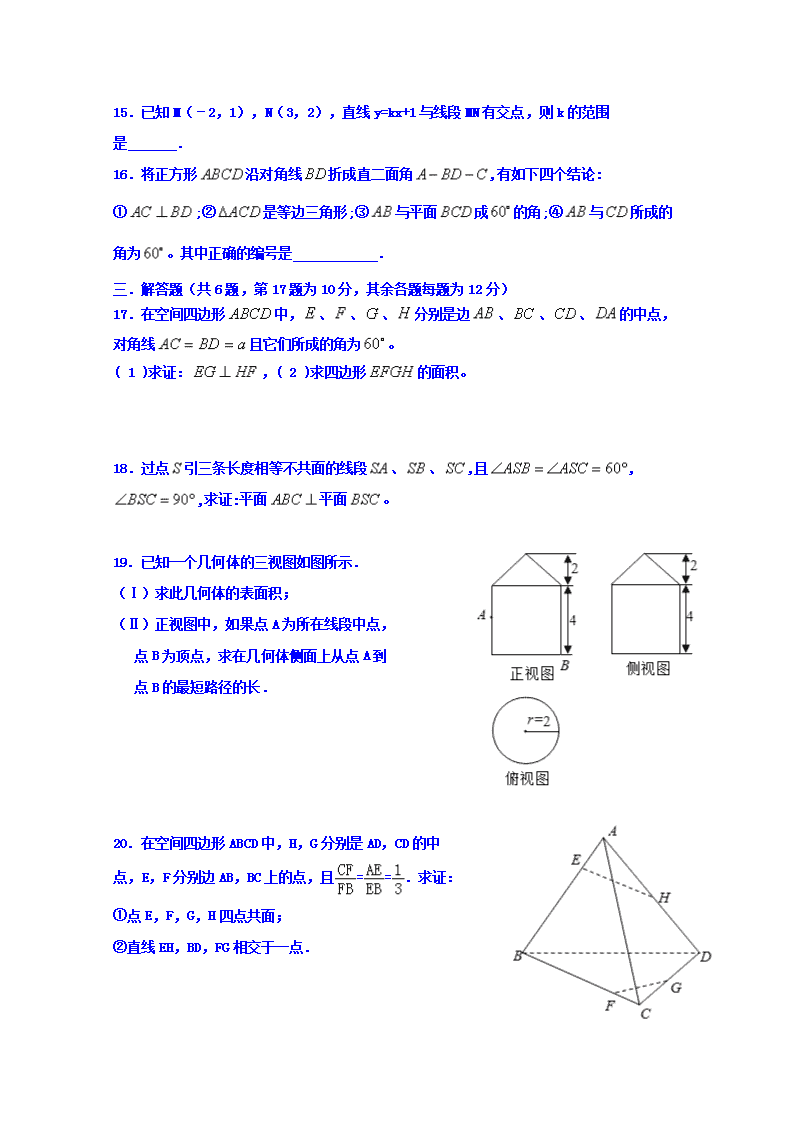
19. 已知一个几何体的三视图如图所示.
(Ⅰ)求此几何体的表面积;
(Ⅱ)正视图中,如果点A为所在线段中点,
点B为顶点,求在几何体侧面上从点A到
点B的最短路径的长.
20. 在空间四边形ABCD中,H,G分别是AD,CD的中
点,E,F分别边AB,BC上的点,且==.求证:
①点E,F,G,H四点共面;
②直线EH,BD,FG相交于一点.
21.已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD,点E为AB中点,点F为PD中点.
( 1 )证明:平面PED⊥平面PAB;
( 2 )求二面角P-AB-F的平面角的余弦值.
22.如图,四棱锥PABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=,M为BC上一点,且BM=.
(1)证明:BC⊥平面POM;
(2)若MP⊥AP,求四棱锥PABMO的体积.
高二月考一理数答案2018.9
1
2
3
4
5
6
7
8
9
10
11
12
D
B
D
B
D
B
C
C
B
C
D
D
13. 三或四 14. 平行或相交或异面 15. k≤0或 16. ①②④
17.解:⑴在中,、分别是边、的中点,
∴∥,
在中,、分别是边、的中点,
∴∥,
∴∥且,
同理:∥且,
∵,∴,
∴四边形为菱形,∴。
⑵∵∥,∥,
∴(或的补角)即为异面直线与所成的角,
由已知得:四边形的面积为:。
18.证明:作平面,为垂足,
∵,,
∴,同理,
∴,
∴为△的外心,
又,
故为中点,
即在平面内,
所以平面平面。
19.解:(Ⅰ)由三视图知:该几何体是一个圆锥与圆柱的组合体,
其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和;
则S圆锥侧=×(2π×2)•(2)=4π,
S圆柱侧=(2π×2)×4=16π,
S圆柱底=π•22=4π,
所以S表面积=4π+16π+4π=4π+20π;…(6分)
(Ⅱ)沿A点与B点所在母线剪开圆柱侧面,如图所示:
则AB===2,
所以从A点到B点在侧面上的最短路径的长为2.(12分)
20. 证明:①如图所示,
空间四边形ABCD中,H,G分别是AD,CD的中点,∴HG∥AC;
又==,∴EF∥AC,∴EF∥HG,E、F、G、H四点共面;
②设EH与FG交于点P,
∵EH⊂平面ABD
∴P在平面ABD内,
同理P在平面BCD内,
且平面ABD∩平面BCD=BD,
∴点P在直线BD上,
∴直线EH,BD,FG相交于一点.
21(1)证明:连BD.∵AB=AD,∠DAB=60°,
∴△ADB为等边三角形,∴E是AB中点.∴AB⊥DE,∵PD⊥面ABCD,
AB面ABCD,∴AB⊥PD.
∵DE面PED,PD面PED,DE∩PD=D,
∴AB⊥面PED,∵AB面PAB.∴面PED⊥面PAB.
(2)解:∵AB⊥平面PED, PE面PED,∴AB⊥PE.连结EF,∵ EF面PED,∴AB⊥EF.∴ ∠PEF为二面角P-AB-F的平面角.
设AD=2,那么PF=FD=1,DE=.
在△PEF中,PE=,EF=2,PF=1
∴cos∠PEF=
即二面角P-AB-F的平面角的余弦值为.
22.. 解:(1)证明:如图,因为四边形ABCD为菱形,O为菱形中心,连接OB,AM,则AO⊥OB.因为∠BAD=,
故OB=AB·sin∠OAB=2sin=1,
又因为BM=,且∠OBM=,在△OBM中,
OM2=OB2+BM2-2OB·BM·cos∠OBM
=12+2-2×1××cos=.
所以OB2=OM2+BM2,故OM⊥BM.
又PO⊥底面ABCD,所以PO⊥BC.从而BC与平面POM内两条相交直线OM,OP都垂直,
所以BC⊥平面POM.
(2)由(1)可得,OA=AB·cos∠OAB=2×cos=.
设PO=a,由PO⊥底面ABCD知,△POA为直角三角形,故PA2=PO2+OA2=a2+3.
由△POM也是直角三角形,
故PM2=PO2+OM 2=a2+.
在△ABM中,
AM2=AB2+BM2-2 AB·BM·cos∠ABM
=22+2-2×2××cos=.
由已知MP⊥AP,故△APM为直角三角形,则
PA2+PM2=AM 2,即a2+3+a2+=,得a=,a=-(舍去),
即PO=.
此时S四边形ABMO=S△AOB+S△OMB=·AO·OB+·BM·OM=××1+××=.
所以四棱锥PABMO的体积
VPABMO=·S四边形ABMO·PO=××=.