- 111.20 KB
- 2024-01-26 发布
数学试卷
一、选择题(本大题共12小题,共60.0分)
1. 为了调查某工厂生产的一种产品的尺寸是否合格,现从500件产品中抽出10件进行检验先将500件产品编号为000,001,002,⋯,499,在随机数表中任选一个数开始,例如选出第6行第8列的数4开始向右读(为了便于说明,下面摘取了随机数表,附表1的第6行至第8行),即第一个号码为439,则选出的第4个号码是( )
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75
A. 548 B. 443 C. 379 D. 217
2. 某学校有高一、高二、高三三个年级,已知高一、高二、高三的学生数之比为2∶3∶5,现从该学校中抽取一个容量为100的样本,从高一学生中用简单随机抽样抽取样本时,学生甲被抽到的概率为14,则该学校学生的总数为( )
A. 200 B. 400 C. 500 D. 1000
3. 从装有3个白球,1个红球(球除颜色外完全相同)的不透明箱子中,不放回地随机取出了3个球,恰好是2个白球,1个红球的概率是( )
A. 34 B. 13 C. 12 D. 16
4. 某校有1000人参加某次模拟考试,其中数学考试成绩近似服从正态分布N105,σ2σ>0,试卷满分150分,统计结果显示数学成绩优秀(高于120分)的人数占总人数的15,则此次数学考试成绩在90分到105分之间的人数约为( )
A. 150 B. 200 C. 300 D. 400
5. 200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速的众数、中位数的估计值为( )
A. 62,62.5 B. 65,62 C. 65,63.5 D. 65,65
6. 已知变量x,y之间的线性回归方程为y=-0.5x+15,且变量x,y之间的一组关系数据如下表所示,则下列说法中,正确的个数是( )
x
2
4
6
8
y
14
m
12
11
①当x=12时,y的值必定为9;
②变量x,y负相关;
③由表格数据知,该回归直线必过点(5,12.5);
④m=12.
A. 1 B. 2 C. 3 D. 4
1. 4名学生和3位老师排成一排合影,恰有两位老师相邻的不同排法有( )
A. 240种 B. 2880种 C. 720种 D. 960种
2. 已知(x-1)5=a0+a1(x+1)+a2(x+1)2+…+a5(x+1)5,则a2=( )
A. 20 B. -20 C. 80 D. -80
3. 已知数据x1,x2,…,x10,2的平均数为2,方差为1,则数据x1,x2,…,x10相对于原数据( )
A. 一样稳定 B. 变得比较稳定
C. 变得比较不稳定 D. 稳定性不可以判断
4. 从3,5,7中选两个数字,从0,4,6中选两个数字,组成无重复数字的四位数.其中偶数的个数为( )
A. 36个 B. 72个 C. 82个 D. 96个
5. 3x-23x11的展开式中有理项共有( )
A. 4项 B. 3项 C. 2项 D. 1项
6. 某中学为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的PK赛.A,B两队各由4名选手组成,一共进行4局比赛,每局两队各派1名选手进行PK,除第3局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为23,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
A. 2027 B. 5281 C. 1627 D. 79
二、填空题(本大题共4小题,共20.0分)
7. 已知随机变量ξ服从正态分布,N1,2,则D2ξ+3=________.
8. (1-2x)5的展开式中含x3的项的系数为________;所有项的系数和为________·
9. 位于数轴原点的一只电子兔沿着数轴按下列规则移动:电子兔每次移动一个单位,移动的方向向左或向右,并且向左移动的概率为23,向右移动的概率为13,则电子兔移动五次后位于点(-1,0)的概率是________.
10. “2019曹娥江国际半程马拉松”在上虞举行,现要选派5名志愿者服务于A、B、C、D四个不同的运动员救助点,每个救助点至少分配一人,若志愿者甲要求不到A救助点,则不同的分配方案有 种.
三、解答题(本大题共6小题,共70.0分)
11. (10分)甲、乙两班各派三名同学参加知识竞赛,每人回答一个问题,答对得10分,答错得0分,假设甲班三名同学答对的概率都是23,乙班三名同学答对的概率分别是23,23,12,且这六名同学答题正确与否相互之间没有影响.
(1)记“甲、乙两班总得分之和是60分”为事件A,求事件A发生的概率;
(2)用X表示甲班总得分,求随机变量X的概率分布和数学期望.
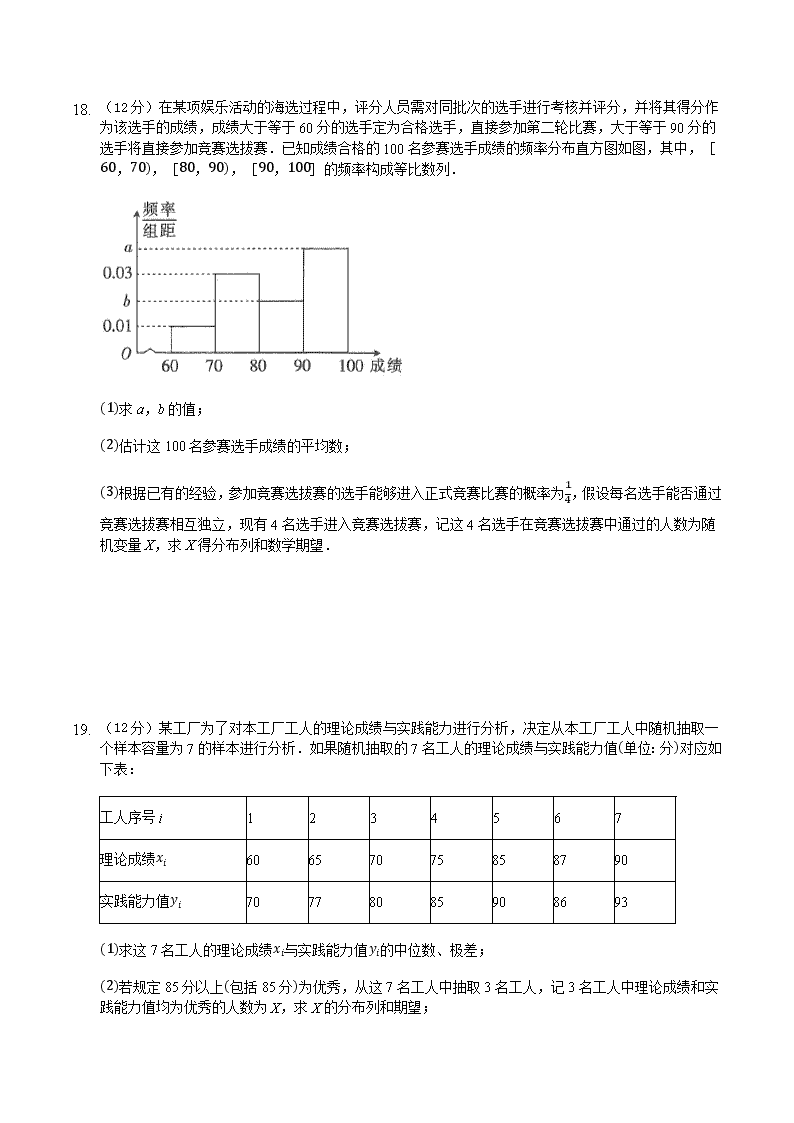
1. (12分)在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,大于等于90分的选手将直接参加竞赛选拔赛.已知成绩合格的100名参赛选手成绩的频率分布直方图如图,其中,[60,70),[80,90),[90,100]的频率构成等比数列.
(1)求a,b的值;
(2)估计这100名参赛选手成绩的平均数;
(3)根据已有的经验,参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为14,假设每名选手能否通过竞赛选拔赛相互独立,现有4名选手进入竞赛选拔赛,记这4名选手在竞赛选拔赛中通过的人数为随机变量X,求X得分布列和数学期望.
2. (12分)某工厂为了对本工厂工人的理论成绩与实践能力进行分析,决定从本工厂工人中随机抽取一个样本容量为7的样本进行分析.如果随机抽取的7名工人的理论成绩与实践能力值(单位:分)对应如下表:
工人序号i
1
2
3
4
5
6
7
理论成绩xi
60
65
70
75
85
87
90
实践能力值yi
70
77
80
85
90
86
93
(1)求这7名工人的理论成绩xi与实践能力值yi的中位数、极差;
(2)若规定85分以上(包括85分)为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
(3)根据下表数据,求实践能力值y关于理论成绩x的线性回归方程.(系数精确到0.01)
附:线性回归方程y=bx+a中,b=i=1n(xi-x)(yi-y)i=1n(xi-x)2,a=y-bx.
x
y
i=17xi-x2
i=17xi-xyi-y
76
83
812
526
1. (12分)为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市为拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度,对年龄在20∼60岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下:
年龄
[20,28)
[28,36)
[36,44)
[44,52)
[52,60)
支持的人数
15
5
15
28
17
(1)由以上统计数据填2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异;
44岁以下
44岁及44岁以上
总计
支持
不支持
总计
(2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会.现从这8人中随机抽2人.
①抽到1人是44岁以下时,求抽到的另一人是44岁以上的概率.
②记抽到44岁以上的人数为X,求随机变量X的分布列及数学期望.
参考数据:
P(K2≥k0)
0.100
0.050
0.010
0.001
k0
2.706
3.841
6.635
10.828
K2=nad-bc2a+bc+da+cb+d,其中n=a+b+c+d.
1. (12分)为增强学生体质,合肥一中组织体育社团,某班级有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.
(1)求这4人中恰有1人参加篮球社团的概率;
(2)用ξ,η分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为ξ和η之差的绝对值,求随机变量X的分布列与数学期望E(X).
1. (12分)某小店每天以每份5元的价格从食品厂购进若干份食品,然后以每份10元的价格出售.如果当天卖不完,剩下的食品还可以每份1元的价格退回食品厂处理.
(Ⅰ)若小店一天购进16份,求当天的利润y(单位:元)关于当天需求量n(单位:份,n∈N)的函数解析式;
(Ⅱ)小店记录了100天这种食品的日需求量(单位:份),整理得下表:
日需求量 n
14
15
16
17
18
19
20
频数
10
20
16
16
15
13
10
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)小店一天购进16份这种食品,X表示当天的利润(单位:元),求X的分布列及数学期望;
(ii)以小店当天利润的期望值为决策依据,你认为一天应购进食品16份还是17份?
数学试卷
【答案】
1. D 2. B 3. A 4. C 5. D 6. B 7. B
8. D 9. C 10. D 11. C 12. A
13. 8
14. -80;-1
15. 80243
16. 180
17. 解:(1)P(A)=(23×23×23)×(23×23×12)=16243;
(2)随机变量X的取值为0,10,20,30.
P(X=0)=C30(1-23)3=127,
P(X=10)=C31(1-23)2×23=29,
P(X=20)=C32(23)2×(1-23)=49,
P(X=30)=C33(23)3=827,
所以,X的概率分布为:
X
0
10
20
30
P
127
29
49
827
所以期望E(X)=0×127+10×29+20×49+30×827=20.
18. 解:(1)由题意,0.01+0.03+a+b×10=10.01a=b2
解得a=0.04b=0.02
(2)估计这100名选手的成绩平均数为65×0.1+75×0.3+85×0.2+95×0.4=84.
(3)由题意知,X∼B(4,14),
则X可能取值为0,1,1,2,3.
则P(X=i)=C4i(1-14)4-i(14)i.
所以X的分布列为:
X
0
1
2
3
4
P
81256
2764
27128
364
1256
故X的数学期望为E(X)=4×14=1.
19. 解:(1)这7名工人的理论成绩xi的中位数为75,
极差为90-60=30;
实践能力值yi的中位数为85,极差为93-70=23.
(2)∵7名工人中理论成绩和实践能力值均为优秀的人数为3名,
∴X的所有可能取值为0,1,2,3,
则,
,
,
.
∴X的分布列为
X
0
1
2
3
P
435
1835
1235
135
∴E(X)=0×435+1×1835+2×1235+3×135=97.
(3)由公式得b=i=17(xi-x)(yi-y)i=17(xi-x)2=263406≈0.65,
a=y-bx=83-263406×76≈33.77.
∴实践能力值y关于理论成绩x的线性回归方程为y=0.65x+33.77.
20. 解:(1)由统计数据填2×2列联表如下,
44岁以下
44岁及44岁以上
合计
支持
35
45
80
不支持
15
5
20
合计
50
50
100
计算观测值k0=100×(35×5-45×15)250×50×80×20=254=6.25>3.841,
所以在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异;
(2)由题意可知抽取的这8人中,44岁以下的有6人,44岁以上的有2人,
①抽到1人是44岁以下的概率为68=34,抽到1人是44岁以下且另一人是44岁以上的概率为.
故所求概率为3734=47.
②根据题意,X的可能取值是0,1,2;
计算P(X=0)=C62C82=1528,
P(X=1)=C61⋅C21C82=37,
P(X=2)=C22C82=128,
可得随机变量X的分布列为
X
0
1
2
P
1528
37
128
故数学期望为E(X)=0×1528+1×37+2×128=12.
21. 解:(1)依题意,这4个人中,每个人参加篮球社团的概率为13,
参加足球社团的概率为23,
设“这4个人中恰有i个人参加篮球社团”为事件Ai(i=0,1,2,3,4),
则P(Ai)=C4i(13)i(23)4-i,(i=0,1,2,3,4),
这4个人中恰有1个人参加篮球社团的概率为:
P(A1)=C41(13)(23)3=3281;
(2)由已知得X的所有可能取值为0,2,4,
P(X=0)=C42(13)2(23)2=2481=827,
P(X=2)=C41(13)(23)3+C43(13)3(23)=4081,
P(X=4)=C40(23)4+C44(13)4=1781,
∴X的分布列为:
∴E(X)=0×827+2×4081+4×1781=14881.
22. 解:(Ⅰ)当日需求量n≥16时,利润y=80,
当日需求量n<16时,利润y=5n-4(16-n)=9n-64,
所以y关于n的函数解析式为y=9n-64,n<16,80,n⩾16(n∈N).
(Ⅱ)(i)X可能的取值为62,71,80,
并且,P(X=71)=0.2,P(X=80)=0.7.
X的分布列为:
X
62
71
80
P
0.1
0.2
0.7
X的数学期望为E(X)=62×0.1+71×0.2+80×0.7=76.4元.
(ii)若小店一天购进17份食品,Y表示当天的利润(单位:元),
那么Y的分布列为:
Y
58
67
76
85
P
0.1
0.2
0.16
0.54
Y的数学期望为E(Y)=58×0.1+67×0.2+76×0.16+85×0.54=77.26元.
由以上的计算结果可以看出,E(X)120=PX<90=15,
∴P105≤X≤120=P90≤X≤105=310,
因此,此次数学考试成绩在90分到105分之间的人数约为1000×310=300,
故选C.
5. 【分析】
本题考查频率分布直方图,众数、中位数,属于基础题.
根据频率分布直方图,进行求解即可.
【解析】
解:最高的矩形为第三个矩形,所以时速的众数为65,
前两个矩形的面积为(0.01+0.02)×10=0.3,
由于0.5-0.3=0.2,
∴中位数为60+0.20.04=65.
故选D.
6. 【分析】
本题考查了线性回归方程经过样本中心的特点以及回归直线方程的意义,属于基础题.
求出x-,代入回归方程解出y-,列方程解出m,再判断每个选项是否正确.
【解答】
解:当x=12时,y=-0.5×12+15=9,回归方程只是一种预测值,不是精确值,所以①错误;
线性回归方程为y=-0.5x+15,b=-0.5<0,所以变量x,y之间呈负相关关系,所以②正确;
x-=2+4+6+84=5,y-=-0.5×5+15=12.5,故该回归直线必过点(5,12.5),故③正确;
又14+m+12+114=12.5,解得m=13,故④错误;
所以正确的有2个.
故选B.
7. 【分析】
本题是排列组合的综合问题,考查分步乘法原理.恰有两位老师相邻,用捆绑插空法来解决问题.先将所有学生排列,然后将3位老师中2位捆绑一起,再与另一个老师插入到2个空中,根据分步乘法原理即可计算结果.
【解答】
解:用捆绑法与插空法解决问题,将所有学生先排列,有A44种排法,
然后将3位老师中2位捆绑一起,有A32种方法,
再与另一个老师插入到2个空中,有A52种方法,
共有A44·A32·A52=2880种排法,
故选B.
8. 【分析】
本题主要考查二项式定理的应用,属于基础题.
把(x-1)5变为[(x+1)-2]5,利用二项式定理展开即可.
【解答】
解:(x-1)5=[(x+1)-2]5=[-2+(x+1)]5,
所以a2=C52-23=-80.
故选D.
9. 【分析】
本题考查的是平均值、方差的计算公式,属基础题.
先根据11个数据的方差为1计算出 i=110xi-22=11,即可得出答案.
【解答】
解:∵数据x1,x2,···,x10,2的平均值为2,
∴数据x1,x2,···,x10的平均值也为2,
∵数据x1,x2,···,x10,2的方差为1,
∴111i=110(xi-2)2+(2-2)2=1,
∴i=110(xi-2)2=11,
∴数据x1,x2,···,x10的方差为110i=110(xi-2)2=1.1,
∵1.1>1,
∴数据x1,x2,···,x10相对于原数据变得比较不稳定,
故选C.
10. 【分析】
本题考查排列知识,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.分类讨论,分0是否取到,由此可得结论.
【解答】
解:从3,5,7中选两个数字,共有3种取法
从0,4,6中选两个数字,假设没有取到0,即取4、6,末位是4或6,两种放法,故偶数共有3×2×A33=36个
假设取到了0,另一个偶数的选取有两种取法,故偶数共有3×2×2×A33-3×2×A22=60个
故偶数共有36+60=96个
故选D.
11. 【分析】
本题考查二项式中有理数的项数,属于基础题.
利用二项式定理,可得展开式的通项公式为Tr+1=C11r⋅311-r⋅(-2)r⋅x33-r6,其中0⩽r⩽11,且r∈N.令33-r6为整数,可得r=3,9,即可得.
【解答】
解: 3x-23x11的展开式的通项公式为Tr+1=C11r⋅311-r⋅-2r⋅x33-r6,其中0≤r≤11,且r∈N.
令33-r6为整数,可得r=3,9,故展开式中有理项共有2项.
故选C.
12. 【分析】本题主要考查了互斥事件,相互独立事件,属于中档题.
比赛结束时A队的得分高于B队的得分可分为两种情形: ①A队在第3局失败,在第1局、第2局、第4局均获胜; ②A队在第3局获胜,且在其他3局中至少胜1局.利用公式求解即可.
【解答】解:设第i局A队获胜为事件Ai(i=1,2,3,4),比赛结束时A队的得分高于B队的得分为事件C.
可分为两种情形:
①A队在第3局失败,在第1局、第2局、第4局均获胜;
②A队在第3局获胜,且在其他3局中至少胜1局.
所以P(C)=P(A1A2A3A4)+P(A3)[1-P(A1A2A4)]
=23×23×(1-23)×23+23×[1-(1-23)×(1-23)×(1-23)]
=881+5281=2027.
故选A.
13. 【分析】
本题考查正态分布的概念和应用,属基础题.
根据正态分布的表示和方差的意义求解.
【解答】
解:随机变量ξ服从正态分布,N(1,2),
∴Dξ=2,
∴D(2ξ+3)=22Dξ=8.
故答案为8.
14. 【分析】本题考查了二项展开式的特定项与特定项的系数和二项式定理的应用,先得出二次展开式的通项,可得x3的项的系数,令x=1,可得所有项的系数和.
【解答】
解:Tr+1=C5r-2rxr,令r=3,则T4=-80x3,
所以含x3的项的系数为-80,设(1-2x)5=a0+a1x+…+a5x5,
令x=1,则a0+a1+…+a5=-1,所以所有项的系数和为-1.
15. 【分析】
本题考查n次独立重复试验中恰有k次发生的概率计算,关键是明确质点P移动5次后位于点(-1,0)质点在移动过程中向右移动2次向左移动3次,再利用公式计算概率可求.
【解答】
解:根据题意,质点P移动五次后位于点(-1,0),其中向左移动3次,向右移动2次;其中向左平移的3次有C 53种情况,剩下的2次向右平移;
则其概率为C 53×132×233=80243.
故答案为80243.
16. 【分析】
本题考查计数原理和排列、组合的应用,考查推理能力和计算能力,属于一般题.
解法一:先不考虑志愿者甲的限制条件,再剔除志愿者甲在A救助点的情况,即可求解;
解法二:(优先考虑甲)分两类:甲单独一人分配到某救助点(A救助点除外)和甲与另外一名志愿者一同被分配到某救助点(A救助点除外),即可求解;
解法三:(优先考虑A救助点)分两类:A救助点安排一人和A救助点安排两人,即可求解.
【解答】
解:解法一:先不考虑志愿者甲的限制条件,
则有C52·A44=240种,再剔除志愿者甲在A救助点的情况,
(1)只有志愿者甲在A救助点:C42A33=36种;
(2)甲及另一人在A救助点:C41A33=24种.
所以不同的分配方案有240-36-24=180种.
解法二:(优先考虑甲)分两类:
(1) 甲单独一人分配到某救助点(A救助点除外):C31C42A33=108种;
(2) 甲与另外一名志愿者一同被分配到某救助点(A救助点除外):C41C31A33=72种,
共108+72=180种.
解法三:(优先考虑A救助点)分两类:
(1)A救助点安排一人:C41C42A33=144种;
(2)A救助点安排两人:C42A33=36种,
共144+36=180种.
17. 本题考查了相互独立与二项分布列的概率计算公式分布列及其数学期望,考查了推理能力与计算能力,属于基础题.
(1)利用相互独立概率计算公式即可得出.
(2)随机变量X的可能取值是0,10,20,30,利用二项分布列的概率计算公式即可得出,进而得出随机变量X的数学期望E(X).
18. 本题考查了频率分布直方图的应用,离散型随机变量的分布列,属于中档题.
(1)本小题考查频率分布直方图的应用,利用等比数列的性质,求出a,b的值;
(2)利用频率分布直方图解决平均数,即可得;
(3)本小题考查离散型随机变量的分布列及其数学期望,利用二项分布,即可求出随机变量的分布列和数学期望.
19. 本题主要考查离散型随机变量的分布列和期望以及线性回归方程,考查中位数与极差的概念,考查计算能力,属于中档题.
(1)利用中位数、极差的定义求解即可;
(2)由题意可知X的所有可能取值为0,1,2,3,计算出相应的概率,即可得X的分布列和数学期望.
(3)由表中数据结合公式求得b=i=17(xi-x)(yi-y)i=17(xi-x)2=263406,再求a,即可求解.
20. 本题考查了离散型随机变量的分布列与数学期望的计算问题,也考查了概率计算问题,是中档题.
(1)由统计数据填写列联表,计算观测值,对照临界值得出结论;
(2)①求抽到1人是44岁以下的概率,再求抽到1人是44岁以下且抽到另1人是44岁以上的概率;②根据题意知X的可能取值,计算对应的概率值,写出随机变量X的分布列,计算数学期望值.
21. 本题考查相互独立事件同时发生的概率以及离散型随机变量的分布列和数学期望,属于中档题.
(1)本小题考查独立事件同时发生的概率计算,根据条件首先求出每个人参加篮球社团的概率为13,再利用独立事件同时发生的概率公式得到恰有1人参加篮球社团的概率P(A1)=C41(13)(23)3=3281;
(2)本小题考查离散型随机变量的分布列,根据条件求出X的所有可能取值,并求它们的概率,即可写出其分布列,再根据数学期望公式即可求出数学期望.
22. 本题考查离散型随机变量的分布列和期望,以及在实际中的应用,属中档题,
(Ⅰ)分n≥16和n<16两种情况分别求得利润,写成分段的形式即可得到所求.
(Ⅱ)(i)由题意知X的所有可能的取值为62,71,80,分别求出相应的概率可得分布列和期望;
(ii)由题意得小店一天购进17份食品时,利润Y的所有可能取值为58,67,76,85,分别求得概率后可得Y的分布列和期望,比较EX和E(Y)的大小可得选择的结论.