- 430.50 KB
- 2024-01-23 发布
滑县二中高二数学11月期中试题(理科)
一、选择题(12×5=60分)
1.“”是“数列为递增数列”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.在△ABC中,,,,则BC边上的高等于( )
A. B. C. D.
3.在正方体ABCD﹣A1B1C1D1中,求直线A1B和平面A1B1CD所成的角为( )
A. B. C. D.
4.若数列{an}的通项公式是an=(﹣1)n(3n﹣2),则a1+a2+…+a20=( )
A.30 B.29 C.﹣30 D.﹣29
5. 设△ABC的三内角A、B、C成等差数列,sinA 、sinB、 sinC成等比数列,则这个三角形的形状是( )
A.直角三角形 B.钝角三角形 C.等腰直角三角形 D.等边三角形
6.已知各项为正的等比数列{an}中,a4与a14的等比中项为,则2a7+a11的最小值为( )
A.16 B.8 C. D.4
7.已知数列{an}的通项公式为,则数列{an}( )
A.有最大项,没有最小项 B.有最小项,没有最大项
C.既有最大项又有最小项 D.既没有最大项也没有最小项
8.以原点O引圆(x﹣m)2+(y﹣2)2=m2+1的切线y=kx,当m变化时切点P的轨迹方程( )
A.x2+y2=3 B.(x﹣1)2+y2=3 C.(x﹣1)2+(y﹣1)2=3 D.x2+y2=2
9.若A、B两点的坐标分别是A(3cosa,3sina,1),B(2cosb,2sinb,1),则||的取值范围是( )
A.[0,5] B.[1,5] C.(1,5) D.[1,25]
10.已知有序实数对(x,y)满足条件x≤y≤,则x+y的取值范围是( )
A.[﹣2,] B.[﹣,] C.[﹣1,] D.(﹣∞,]
11.已知O为坐标原点,双曲线的右焦点F,以OF为直径作圆交双曲线的渐近线于异于原点的两点A、B,若,则双曲线的离心率为
A.2 B.3 C. D.
12.已知数列{an}的前n项之和Sn=n2﹣4n+1,则|a1|+|a2|+…+|a10|的值为( )
A.61 B.65 C.67 D.68
二、填空题(4×5=20分)
13.已知方程(是常数)表示曲线,给出下列命题:
①曲线不可能为圆;②曲线不可能为抛物线;
③若曲线为双曲线,则或;④若曲线为焦点在x轴上的椭圆,则.其中真命题的编号为 .
14.在正三棱柱ABC﹣A1B1C1,若AB=2,AA1=1,则A到平面A1BC的距离 .
15.已知数列{an}满足a1=33,an+1﹣an=2n,则的最小值为 .
16.设是外接圆的圆心,分别为角对应的边,已知
,则的范围是_________________.
三、解答题
17.(本小题满分10分)已知.
(I)当时,p为真命题且非q为真命题,求x的取值范围;
(Ⅱ)若p是q的充分条件,求实数m的取值范围.
18.(本小题满分12分)如图,直三棱柱ABC﹣A1B1C1内接于高为的圆柱中,已知∠ACB=90°,AA1=,BC=AC=1,O为AB的中点.求:
(1)圆柱的全面积;
(2)异面直线AB′与CO所成的角的大小;
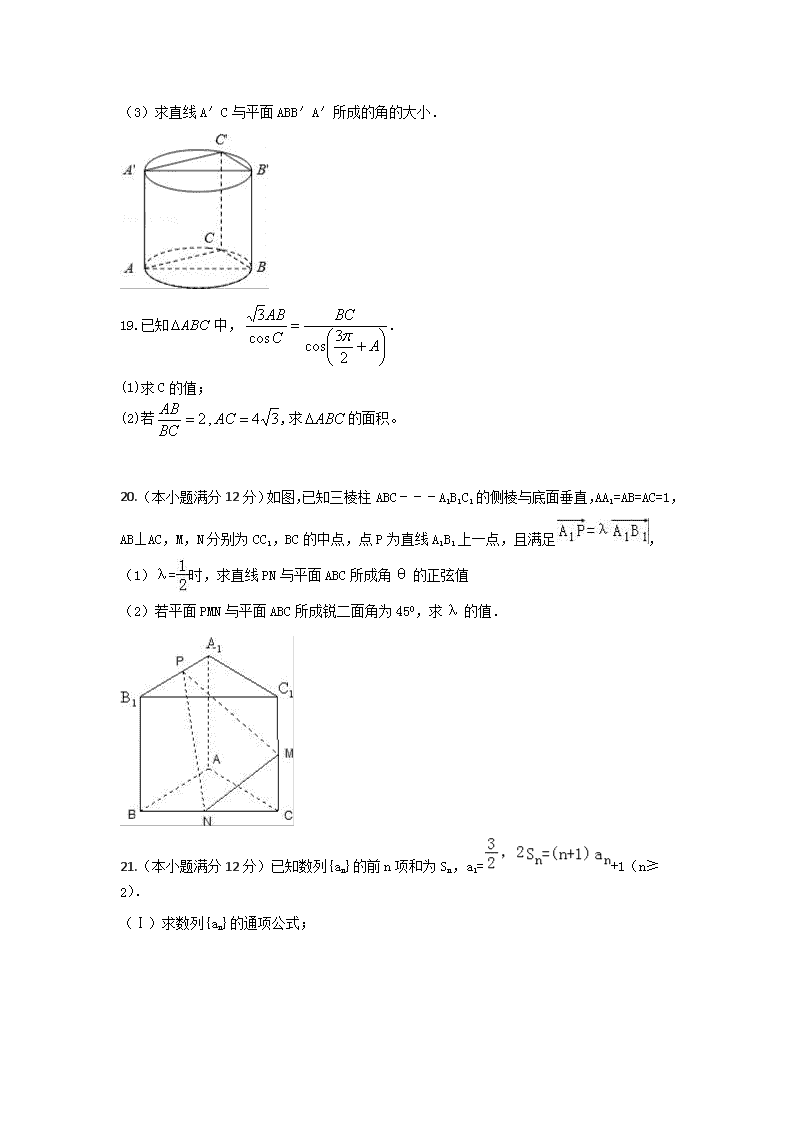
(3)求直线A′C与平面ABB′A′所成的角的大小.
19. 已知中,.
(1) 求C的值;
(2) 若,求的面积。
20.(本小题满分12分)如图,已知三棱柱ABC﹣﹣﹣A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别为CC1,BC的中点,点P为直线A1B1上一点,且满足,
(1)λ=时,求直线PN与平面ABC所成角θ的正弦值
(2)若平面PMN与平面ABC所成锐二面角为450,求λ的值.
21.(本小题满分12分)已知数列{an}的前n项和为Sn,a1=+1(n≥2).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=,数列{bn}的前n项和为Tn,证明:Tn<.
22.(本小题满分12分)已知椭圆的左焦点为,离心率为。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设为坐标原点, 为直线上一点,过作的垂线交椭圆于,。当四边形是平行四边形时,求四边形的面积。
试卷答案
1.A 2.B 3.B
【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD﹣A1B1C1D1的棱长为1,
则A1(1,0,1),B(1,1,0),D(0,0,0),C(0,1,0),
=(0,1,﹣1),=(1,0,1),=(0,1,0),
设平面A1B1CD的法向量=(x,y,z),
则,取x=1,则=(1,0,﹣1),
设直线A1B和平面A1B1CD所成的角为θ,
sinθ===, ∴θ=,
∴直线A1B和平面A1B1CD所成的角为. 故选:B.
4.A 【解答】解:∵当n为奇数时,
an+an+1=﹣(3n﹣2)+(3(n+1)﹣2)=3,
∴a1+a2+…+a20 =(a1+a2)+(a3+a4)+…+(a19+a20) =3×10=30; 故选:A.
5.D 6.B【解答】解:∵各项为正的等比数列{an}中,a4与a14的等比中项为,
∴a4•a14=(2)2=8, ∴a7•a11=8, ∵a7>0,a11>0,
∴2a7+a11≥2=2=8. 故选B.
7.C【解答】解:
令,则t是区间(0,1]内的值,而=,
所以当n=1,即t=1时,an取最大值,使最接近的n的值为数列{an}中的最小项,
所以该数列既有最大项又有最小项. 故选C.
8.A 【解答】 解:根据题意画出示意图,设圆心为C,
切点P的坐标为P(x,y),则发现图中隐含
条件.|OP|2=|OC|2﹣|PC|2 ∵|OP|2=x2+y2,|OC|2=m2+4,|PC|2=r2=m2+1,
故点P的轨迹方程为x2+y2=3 故选A
9.B
【解答】解:∵A(3cosa,3sina,1),B(2cosb,2sinb,1),
∴=(3cosa﹣2cosb)2+(3sina﹣2sinb)2+(1﹣1)2
=9+4﹣12(cosacosb+sinasinb) =13﹣12cos(a﹣b);
∵﹣1≤cos(a﹣b)≤1, ∴1≤13﹣12cos(a﹣b)≤25, ∴||的取值范围是[1,5].
故选:B.
10.A
【解答】解:有序实数对(x,y)满足条件x≤y≤,表示的平面区域
如图阴影部分:令z=x+y,如图红色直线,
显然,z=x+y经过A时取得最小值,经过B时取得最大值.
A(﹣1,﹣1),B(,). x+y∈[﹣2,].故选:A.
11.C
12.C
【解答】解:当n=1时,S1=a1=﹣2,
当n≥2时,an=Sn﹣Sn﹣1=(n2﹣4n+1)﹣[(n﹣1)2﹣4(n﹣1)+1]=2n﹣5,
故an=,
据通项公式得a1<a2<0<a3<a4<…<a10
∴|a1|+|a2|+…+|a10| =﹣(a1+a2)+(a3+a4+…+a10) =S10﹣2S2
=102﹣4×10+1﹣2(﹣2﹣1) =67. 故选C.
13.②③④
试题分析:对应①,当得,曲线表示的是圆,①错;对应②,方程没有关于的一次项,故曲线不可能是抛物线,正确;对应③,若曲线为双曲线,
得或,③正确;对于④,曲线为焦点在轴上的椭圆,
,得,正确;正确的编号是①②③.
考点:圆锥曲线的判断.
14.【解答】解:设点A到平面A1BC的距离为h,则三棱锥的体积为
即
∴ ∴h=. 故答案为:.
15.【解答】解:an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1=2[1+2+…+(n﹣1)]+33=33+n2﹣n
所以
设f(n)=,令f′(n)=,
则f(n)在上是单调递增,在上是递减的,
因为n∈N+,所以当n=5或6时f(n)有最小值.
又因为,, 所以的最小值为
16.
17.
18.【解答】解:(1)根据题意:底面半径为:r=,
∴S=2πr2+2πrh=3π;
(2)∵CO⊥平面ABB′A′
∴CO⊥AB′ ∴∠COO′=90°
∴异面直线AB′与CO所成的角是90°;
(3)∵CO⊥平面ABB′A′,
∴∠CA′O为直线A′C与平面ABB′A′所成的角,
∵CO=,A′C=,
∴sin∠CA′O==,
∴∠CA′O=arcsin.
19.略
20.【解答】解:(1)建立以A点为空间坐标系原点,AB,AC,AA1所在直线为x轴,y轴,z轴,A(0,0,0),B(1,0,0),C(0,1,0),A1(0,0,1),B1(1,0,1),C1( 0,1,1),M(0,1,),N(,,0)
λ=,P(,0,1),=(0,,﹣1)
平面ABC法向量为=(0,0,1),∴
(2)设P(λ,0,1),=(,﹣,﹣),=(﹣λ,,﹣1),
设平面PMN法向量为,则,
取
平面ABC法向量为(0,0,1),
∴,
∴.
21.【解答】(Ⅰ)解:当n=2时,2S2=3a2+1,解得a2=2,
当n=3时,2S3=4a3+1,解得a3=3.
当n≥3时,2Sn=(n+1)an+1,2Sn﹣1=nan﹣1+1,
以上两式相减,得2an=(n+1)an﹣nan﹣1,
∴,
∴=,
∴;
(Ⅱ)证明:bn==,
当n=1时,,
当n≥2时,,
∴.
∴Tn<.
22.(Ⅰ)由题意可得,
解得c=2,a=,b=.
∴椭圆C的标准方程为;
(Ⅱ)由(Ⅰ)可得F(﹣2,0),
设T(﹣3,m),则直线TF的斜率,
∵TF⊥PQ,可得直线PQ的方程为x=my﹣2.
设P(x1,y1),Q(x2,y2).
联立,化为(m2+3)y2﹣4my﹣2=0,
△>0,∴y1+y2=,y1y2=.
∴x1+x2=m(y1+y2)﹣4=.
∵四边形OPTQ是平行四边形,
∴,∴(x1,y1)=(﹣3﹣x2,m﹣y2),
∴,解得m=±1.
此时四边形OPTQ的面积S=═=2.
略