- 725.00 KB
- 2024-01-23 发布
江苏省泰州中学2017-2018学年度月度检测
高三(数学)试卷(文科)
一、填空题(每题5分,满分70分,将答案填在答题纸上)
1.若集合,则 .
2.若(为虚数单位),则的值为 .
3.某高校甲、乙、丙、丁四个专业分别有名学生.为了解学生的就业倾向,用分层抽样的方法从该校这四个专业中抽取名学生进行调查,则应从丙专业抽取的学生人数为 .
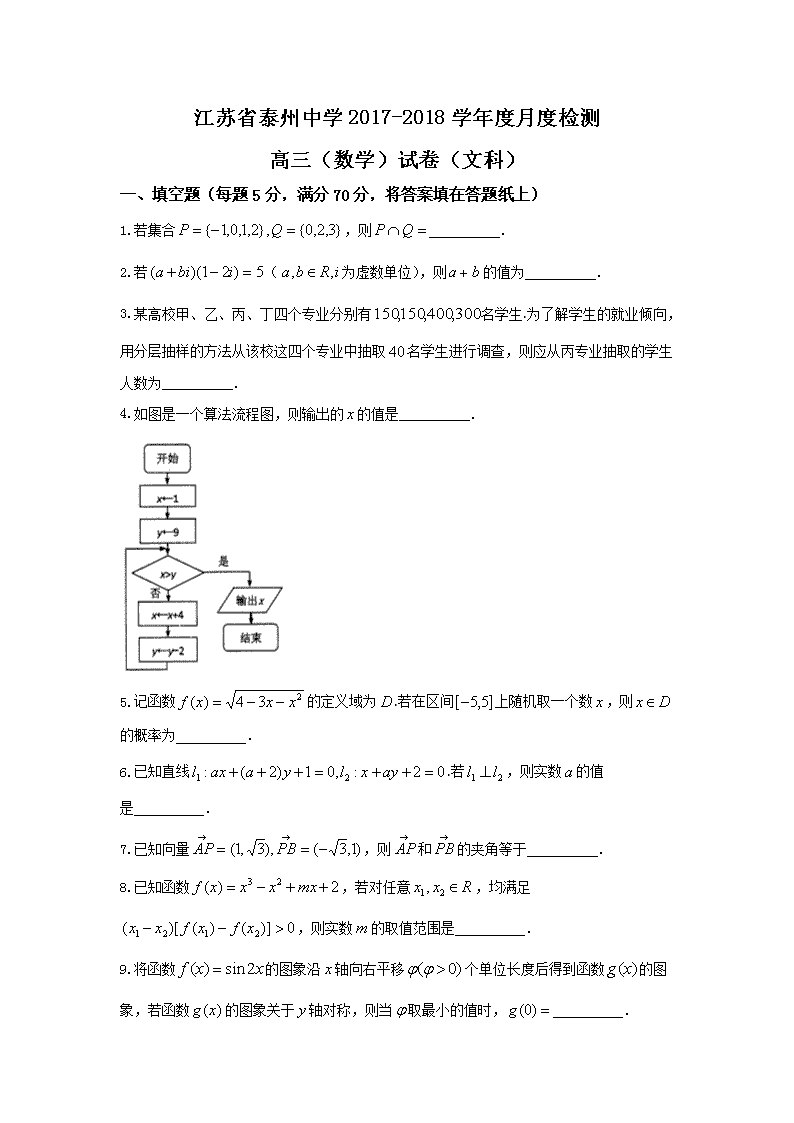
4.如图是一个算法流程图,则输出的的值是 .
5.记函数的定义域为.若在区间上随机取一个数,则的概率为 .
6.已知直线.若,则实数的值是 .
7.已知向量,则和的夹角等于 .
8.已知函数,若对任意,均满足,则实数的取值范围是 .
9.将函数的图象沿轴向右平移个单位长度后得到函数的图象,若函数的图象关于轴对称,则当取最小的值时, .
10.如图,在梯形中,.若,则 .
11.已知动圆与直线相切于点,圆被轴所截得的弦长为,则满足条件的所有圆的半径之积是 .
12.已知,且,则的最小值是 .
13.若函数(为常数,是自然对数的底)恰有两个极值点,则实数的取值范围是 .
14.在中,角所对的边分别为,若为锐角三角形,且满足,则的取值范围是 .
二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)
15. 如图,在中,.
(1)求的值;
(2)设点在以为圆心,为半径的圆弧上运动,且,其中.求的取值范围.
16. 已知函数.
(1)若不等式在上恒成立,求实数的取值范围;
(2)解不等式.
17. 在中,内角所对的边分别为,.
(1)若,求的值;
(2)若,求的值.
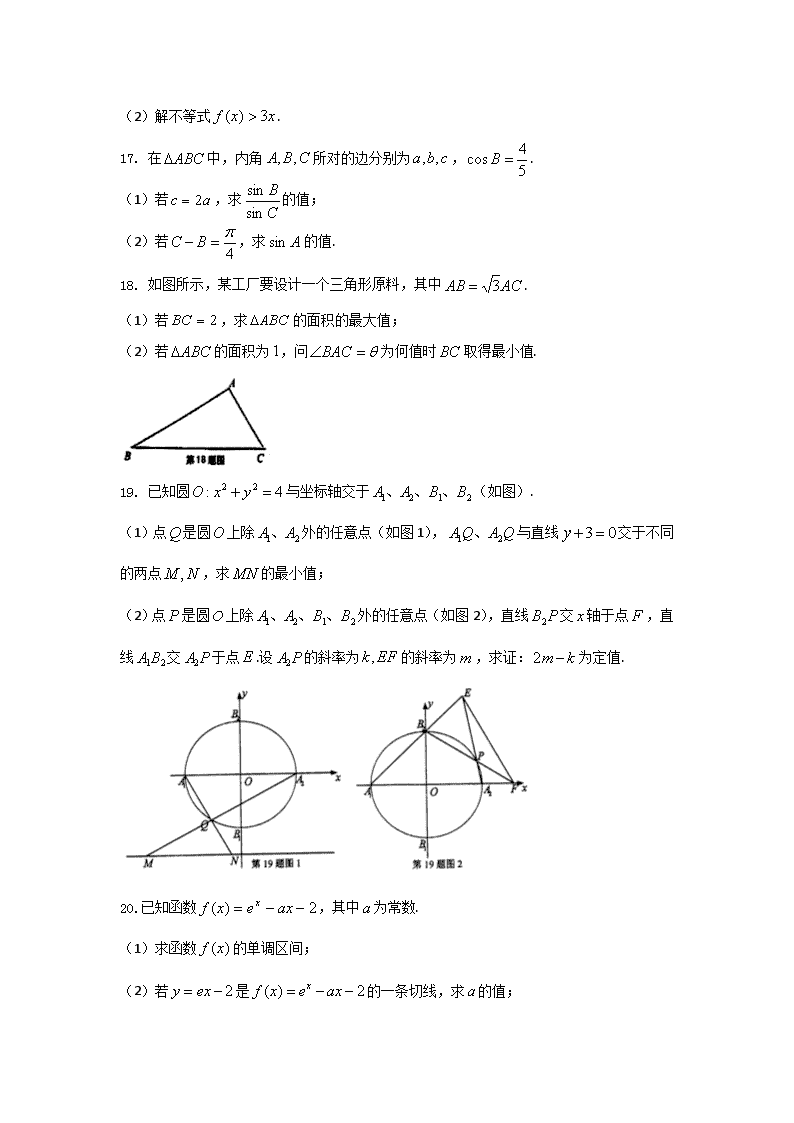
18. 如图所示,某工厂要设计一个三角形原料,其中.
(1)若,求的面积的最大值;
(2)若的面积为,问为何值时取得最小值.
19. 已知圆与坐标轴交于(如图).
(1)点是圆上除外的任意点(如图1),与直线交于不同的两点,求的最小值;
(2)点是圆上除外的任意点(如图2),直线交轴于点,直线交于点.设的斜率为的斜率为,求证:为定值.
20.已知函数,其中为常数.
(1)求函数的单调区间;
(2)若是的一条切线,求的值;
(3)已知为整数,若对任意,都有恒成立,求的最大值.
试卷答案
一、填空题
1. 2. 3. 4. 5. 6. 或 7. 8. 9. 10. 11.
12. 13. 14.
三、解答题
15.(1).
(2)建立如图所示的平面直角坐标,则.
设,
由,
得.
所以.
所以.
.
因为,
所以,当时,即时,的最大值为;
当或即或时,的最小值为.
16.解:(1)当时,.
.于是,即函数在上的最大值等于.
要使不等式在上恒成立,实数的取值范围是.
(2)不等式,即.
当时,原不等式等价于,解得或.又.
当时,原不等式等价于,即,解得,满足.
综上可知,原不等式的解集为或.
17.解:(1)解法1:在中,因为,所以.
因为,所以,即,所以.
又由正弦定理得,所以.
解法2:因为,所以.
因为,由正弦定理得,
所以,即.
又因为,解得,所以.
(2)因为,所以.
又,所以,所以.
因为,即,所以,
所以.
18.解:(1)以所在直线为轴,的中垂线为轴建立直角坐标系,则,
设,由得,
化简得.所以点的轨迹为以为圆心,为半径的圆.(除去与轴的交点)
所以.
(2)设,由得.
令
令得
列表:略
在上单调递减,在上单调递增,
答:当时,有最小值,即最小.
19.解:(1)由题设可以得到直线的方程为,直线的方程为
由,解得;由,解得.
所以,直线与直线的交点,
直线与直线的交点,所以.
当时,,等号成立的条件是.
当时,,等号成立的条件是.
故线段长的最小值是.
(2)由题意可知,
的斜率为直线的方程为,由,得,
则直线的方程为,令,则,即,
直线的方程为,由,解得,
的斜率(定值).
20.解:(1)函数的定义域为.
若时,则,所以在上单调递增;
若时,则当时,,当时,,
所以在上递减,在上递增.
(2)设切点为则:
,解得.
(3)当时,对任意,都有恒成立等价于对恒成立.
令,则,
由(1)知,当时,在上递增.
因为,所以在上存在唯一零点,
所以在上也存在唯一零点,设此零点为,则.
因为当时,,当时,,
所以在上的最小值为,所以
又因为,所以,所以.
又因为为整数且,所以的最大值是.