- 504.79 KB
- 2024-01-20 发布
第1页 共 8 页
2019 安徽省“江南十校”综合素质测试
数学(理科)解析及评分标准
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D A C B D C C A B C B C
1. 答案 D 【解析】 { 2,2}A =− ,故选 D.
2. 答案 A 【解析】 | i | 1 2| | | | |1 i | 22
zz= = = =− ,故选 A.
3. 答案 C 【解析】标准方程为 2 1
2xy= ,故选 C.
4. 答案 B 【解析】由正弦定理知, sin sin 2 2 72cossin sin 3
BC CCC= = = , 7cos ,3C=
2 5cos2 2cos 1 ,9CC = − = 故选 B.
5. 答案D 【解析】 1
2AB AD=, 2+ 3AE AB AD= , BD AB AD= − +
2 1 2 2 1 1( + ) ( ) 13 2 3 3 2 6AE BD AB AD AB AD = − + = − + − = − ,故选 D.
6. 答案 C 【解析】 1 1 1
21= 2ABC A B CVL− 三棱柱 ,故选 C
7 .答案 C 【解析】由已知得, 2 4 = , 1 1 2, ( ) cos( ).2 2 3f x x = = + 故选 C.
8 .答案 A 【解析】由已知得 ( ) ( ), ( )f x f x y f x R− = − =且 在 上单调递增,
22(3log ) (log 1)f x f x −由 可得 223log log 1xx− 2
1log 2x − ,解得: 20.2x 故选 A.
9 .答案 B 【解析】记 (1,0)A ,则
22
2
4|| 2
bcPF a
−== ,
22
1
4| | 2 2
bcPF aa
+= + = , 1| | 1F A c=+,
2| | 1F A c=−,由角平分线性质得 211
22
| | | | 4 0 4| | | |
PF F A c c cPF F A= − = = ,
或作 1AD PF⊥ 于 D ,由角平分线的对称性质知 1 1 1 2| | | | | | | | | | 2 4DF PF PD PF PF a= − = − = = ,
2| | | | 1AD AF c= = − ,在 1Rt ADF 中, 2 2 2
1 1 2| | 1,| | | | | |AF c AF AF AD= + = + ,解得 4c =
故 12
2
1 2 2
14| | | | 24.22PF F
cS F F PF c
−= = = 故选 B.
10 .答案 C 【解析】由已知, min min( ) ( )f x g x ,由已知可得 2
min( ) ( 1) ,f x k=+ min( ) 3gx = ,
2( 1) 3, 4 2 3,kk + − 故选 C.
第2页 共 8 页
11 .答案 B 【解析】由已知得原几何体是由一个棱长为 2 的正方体挖去一个四分之一圆柱
及一个八分之一球体得到的组合体, 2 16 2 4 5 4 20 ,4 8 4S = − − + + = +表 故选 B.
12 .答案 C 【解析】前 44 组共含有数字: 44 (44 1) 1980 + = 个,
1980 44 (2019 1980) 2019 44 1975,S = − + − = − = 故选 C.
二、填空题
题号 13 14 15 16
答案 2 1− 240 57
13. 答案2 【解析】 0, 2xy==时, min 3 0 2 2z = + =
14. 答案 【解析】 22
sin cos 1
sin 4cos 4
=+
, 2
tan 1
4 tan 4
=+
, tan 2 = ,
1 23tan = tan ( ) 11123
−
+ − = = −
+
.
15. 答案 240 【解析】 66( ) = ( )x y z x y z+ + + + ,含 2z 的项为 2 4 2
26T C ( )x y z= + ,所以形如
2abx y z 的项的系数之和为 24
6C 2 =240 .
16.答案 【解析】由已知动点 P 落在以 AB 为轴、底面半径为 21的圆柱的侧面上,该
侧面与三棱锥侧面 ACD 的交线为椭圆的一部分,设其与 AC 的交点为 ,此时 PB 最大,由
到 的距离为 可得 为 的中点,且 2cos ,5BAC=在 BAP 中,由余弦定理可得
22 28 5 2 8 5 575PB = + − = .
三、解答题
17【解析】(1)由 1 2 3 2nna a a a b+ + + + = ①
2n 时, 1 2 3 1 12nna a a a b−−+ + + + = ②
① −②可得: 12( )n n na b b −=−( 2)n ,∴ 3 3 22( ) 8a b b= − =
∵ 1 2, 0naa=,设{}na 公比为 q ,∴ 2
1 8aq = ,∴ 2q = …………………………3 分
∴ 12 2 2nn
na −= =
第3页 共 8 页
∴ 1 2 3 12(1 2 )2 2 2 2 2 2 212
n
nn
nb +−= + + + + = = −− ,∴ 21n
nb =−.…………6 分
(2)证明:由已知: 11
1
2 1 1
(2 1)(2 1) 2 1 2 1
n
n
n n n n n
nn
ac bb ++
+
= = = − − − − −
. ………………9 分
∴ 1 2 3 1 2 2 3 1
1 1 1 1 1 1
2 1 2 1 2 1 2 1 2 1 2 1n nnc c c c ++ + + + = − + − + + −− − − − − −
1
11121n+= − − ………………………………………………………………………………12 分
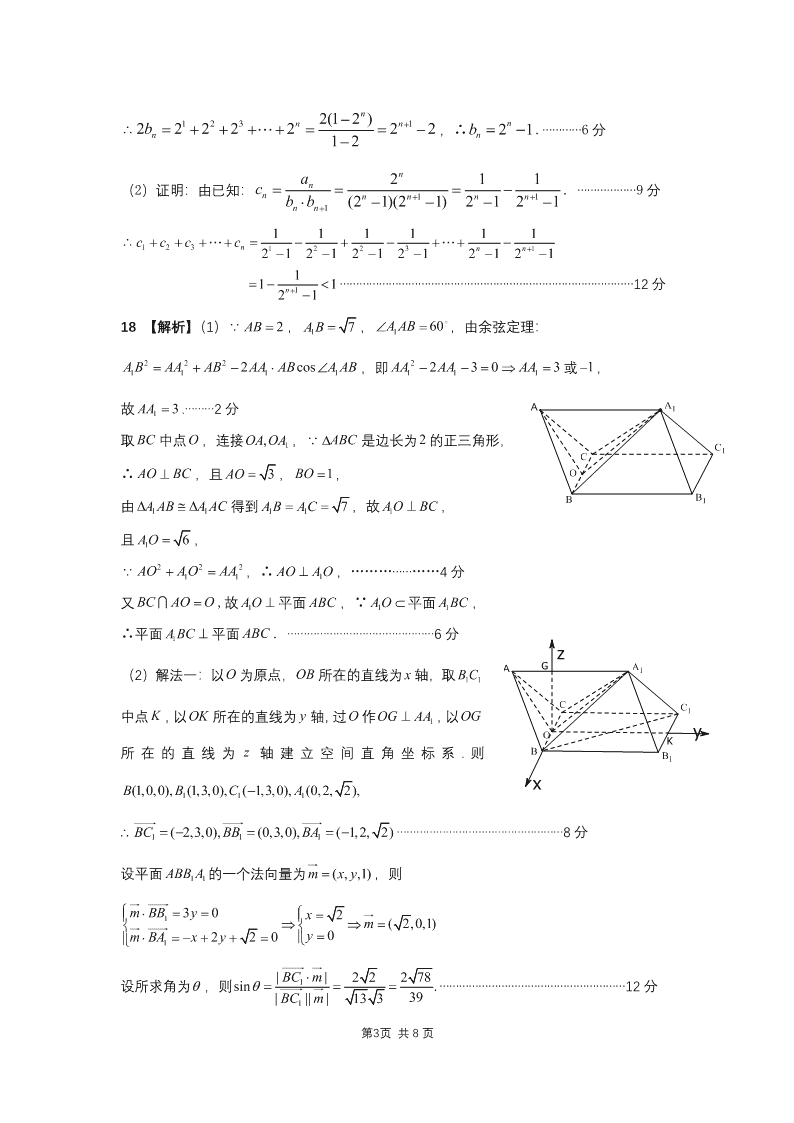
18 【解析】(1)∵ 2AB = , 1 7AB= , 1 60A AB=,由余弦定理:
2 2 2
1 1 1 12 cosA B AA AB AA AB A AB= + − ,即 2
1 1 12 3 0 3AA AA AA− − = = 或 1− ,
故 1 3AA = .………2 分
取 BC 中点O ,连接 1,OA OA ,∵ ABC 是边长为 2 的正三角形,
∴ AO BC⊥ ,且 3AO = , 1BO = ,
由 11A AB A AC 得到 11 7A B AC==,故 1A O BC⊥ ,
且 1 6AO= ,
∵ 2 2 2
11AO AO AA+=,∴ 1AO AO⊥ ,…………………4 分
又 BC AO O= ,故 1AO⊥ 平面 ABC ,∵ 1AO 平面 1A BC ,
∴平面 1A BC ⊥ 平面 ABC . ………………………………………6 分
(2)解法一:以O 为原点,OB 所在的直线为 x 轴,取 11BC
中点 K ,以 OK 所在的直线为 y 轴,过 作 1OG AA⊥ ,以 OG
所在的直线为 z 轴建立空间直角坐标系. 则
1 1 1(1,0,0), (1,3,0), ( 1,3,0), (0,2, 2),B B C A−
1 1 1( 2,3,0), (0,3,0), ( 1,2, 2)BC BB BA = − = = − ……………………………………………8 分
设平面 11ABB A 的一个法向量为 ( , ,1)m x y= ,则
1
1
30 2 ( 2,0,1)
02 2 0
m BB y x m
ym BA x y
= = = == = − + + =
设所求角为 ,则 1
1
||2 2 2 78sin .39| || | 13 3
BC m
BC m
= = = …………………………………………………12 分
A
O
A1
C1
B1B
C
A G
K
z
y
x
C
O
A1
C1
B1
B
第4页 共 8 页
解法二:以O 为原点,OB 所在的直线为 x 轴,以 1OA 所在的直线为 y 轴,以OA 所在的直线
为 z 轴建立空间直角坐标系.则 1(1,0,0), (0,0, 3), (0, 6,0), (1,0,0)B A A C ,设 1( , , )C x y z ,由
11=C A CA可得 1( 1, 6, 3)C −−,
11( 2, 6, 3), (1,0, 3), ( 1, 6,0)BC AB BA = − − = − = − ……………………8 分
设平面 11ABB A 的一个法向量为 ( , , )m x y z= ,则
1
130, 6 ( 6,1, 2)
260
ym AB x z xm
zm BA x y
= = − == == = − + =
取
设所求角为 ,则 1
1
||2 6 2 78sin .39| || | 13 3
BC m
BC m
= = =
…………………………………………………12 分
解法三:由(1) 11 1
1 1 1 23 3 2C ABA AOAV BCS BC AO AO− = = =
设 C 到平面 11ABB A 的距离为 h ,则由 1 1 1//CC ABB A面 知 1C 到平面 的距离也为 ,则
11 1
1 1 1 2 6sin 60 23 3 2 3C ABA ABAV hS h AB A A h− == = = = ………………………………9 分
设所求角为 ,则
1
2 6 2 78sin .3913 3
h
BC = = =
………………………………………………………12 分
19【解析】(1)由数据可知,2012,2013,2016,2017,2018 五个年份考核优秀,故 的所
有可能取值为 0 1 2 3,,,.
03
53
3
8
1( 0) 56
CCP C = = = ,
12
53
3
8
15( 1) ,56
CCP C = = =
2 1 3 0
5 3 5 3
33
88
30 10( 2) , ( 3)56 56
C C C CPPCC= = = = = = ………………………………………………………………4 分
故 的分布列为:
0 1 2 3
P 1
56 15
56 15
28 5
28
所求 1 15 15 5 150 1 2 3 .56 56 28 28 8E = + + + = ………………………………………………………………6 分
第5页 共 8 页
(2)解法一:
8 8 8 22 2 2
1 1 1
( ) 72 ( ) 8 360i i i
i i i
x x x x x x
= = =
− = = − + =
8 8 8
1 1 1
( )( ) 34.5 ( )( ) 8 226.5i i i i i i
i i i
x x y y x y x x y y x y
= = =
− − = = − − + =
故去掉 2015 年的数据之后
6 8 6 4 8 3 296,7 7 7xy − −= = = =
22 2 2 2
55
( ) 7 360 6 7 6 72ii
ii
x x x x
− = − = − − =
55
29( )( ) 7 226.5 6 3 7 6 34.57i i i i
ii
x x y y x y xy
− − = − = − − = …………………………9 分
所以
^ 34.5 0.4872b =,
^^29 34.5 6 1.277 72a y b x= − = −
从而回归方程为:
^
0.48 +1.27.yx= …………………………………………………………………………12 分
解法二: 因为 6 6xx==,所以去掉 2015 年的数据后不影响
^
b 的值,
所以 , …………………………………………………………………………9 分
而去掉 2015 年的数据之后 ,
从而回归方程为: …………………………………………………………………………12 分
注: 若有学生在计算
^
a 时用
^
0.48b 计算得
^^29 0.48 6 1.267a y b x= − = − 也算对。
20【解析】(1)设椭圆C 的标准方程为
22
221( 0)xy abab+ =
由题意得
22 5
3
24
ab
a
b
− =
=
,解得 3
2
a
b
=
=
椭圆 的标准方程为
22
194
xy+=………………4 分
(2)解法一:设 : ( 2 2)l y t t= − 且 0t , 1( , )E x t , 2( , )F x t , 130x, 2 0rx
设 (0, )Ms, A E M、 、 共线 , AM AEkk=
1
00
0 ( 3) ( 3)
st
x
−−=− − − − ,
1
3
3
ts x= + ,得
1
3(0, )3
tM x + ,同理得
1
3N(0, )3
t
x− …………8 分
22
11
33( , t) ( , )33
ttFM FN x x txx = − − − −+−
22
2
11
33( 1)( 1)33xtxx= + − −+−
22
2 2 2 211
2222
1
4
99
xxx t x txt= − = − −
2
2 2 2 2
22
49(9 ) 4 494
tx x t r= − − = + − = −
第6页 共 8 页
12 16FM FN 212 4 16 4 2 5rr − ……………………12 分
解法二:设 1 1 2 2: 3( 0), ( , ), ( , )AE x my m E x y F x y= − ,联立 22
3
194
x my
xy
=− +=
得: 22(4 9) 24 0m y my+ − = ,
2
1
1122
1
24 12 27 4,,4 9 4 9 3 9BE
ymmy x k mm m x
− = = = = −+ + −
4: ( 3)9BN y m x = − − ,令 0x = 得 12(0, )9
mN
又由 : 3( 0)AE x my m= − ,令 得 3(0, )M m …………………………………………8 分
又 //lx轴, 21 2
24
49
myy m = = +
2 2 2
2 2 2 2 2 2 2
3 12 3 12(0 , ) (0 , ) ( ) 4 499
mmFM FN x y x y x y y rmm = − − − − = + − + + = −
12 16FM FN 212 4 16r −
4 2 5r ……………………………………………………………………………………………………12 分
21【解析】(1)证明: 1m = 时, 1( ) lnf x xx=+
22
1 1 1'( ) ( )xf x f xx x x
−= − + = 在(0,1]上递减,在[, 1,2)上递增 ,
min( ) (1) 1, ( ) 1.f x f f x = = …………………………………………………………………4 分
(2)当 0m = 时, ( ) ln , (0,2)f x x x=,明显不满足要求;
当 0m 时,设切点为 00( , ( ))x f x (显然 0 1x ),则有 0
0
0
()'( ) 1
fxfx x= − ,
0
00
2
00
ln
1
mxx m x
xx
+−=− ,整理得 0 2
00
21ln 1 0mmx xx
++ − − = (*)
由题意,要求方程(*)在区间 (0,2) 上有两个不同的实数解.
令 2
21( ) ln 1mmg x x xx
+= + − − , 3
( 2 )( 1)'( ) x m xgx x
−−=
……………………………………6 分
①当 21m 即 1
2m 时, ()gx在(0,1) 上单调递增,在 (1,2) 上单调递减或先单调递减再递增,
而 1( ) ( e 1)(2 e) 0egm= − − , (1) 0gm=, 3 2 1(2) ln 2 1 ln 2 048
mg += + − − ,
1(2 ) ln 2 04g m m m= + ,
()gx 在区间 上有唯一零点,在区间 上无零点,
所以此时不满足题要求.………………………………………………………………………………………………8 分
第7页 共 8 页
②当 0 2 1m即 10 2m时, ()gx在 (0,2 )m 上单调递增,在 (2 ,1)m 上单调递减,在(1,2) 上
单调递增,
(2 1 )( ) ln 1 0, (1) 0,m m m e eg g me e m
+−= + − =
()gx 在区间( )2,0 上有唯一零点,所以此时不满足题要求.………………………10 分
③当 0m 时, 在 ( )1,0 上单调递减,在 上单调递增,
0)2)(1()1( −−= emeeg , 0)1( = mg , 4
232ln)2( −+= mg
当 0)2( g 即 3
2ln42 −m 时, 在区间(0,2) 上有唯一零点,此时不满足题要求.
当 0)2( g 即 03
2ln42 − m 时, 在区间(0,1) 和 上各有一个零点,
设为 21, xx ,又这时 22
1)( x
m
xx
mxxf −=−= 显然在区间 上单调递减,
)()( 21 xfxf 所以此时满足题目要求.
综上所述, m 的取值范围是 2 4ln 2 03 m− .…………………………………………………………12 分
(2)解法二:设切点为 00
0
( , ln )mxxx + ,由解法一的关于 0x 的方程
0
0 2
00
(2 1)1 ln 1 0xmxxx
−+ − + = 在区间内 (0,2) 有两解,显然 1
2 不是方程的解,
故原问题等价于
22ln
12
x x x xm x
+−= − 在区间内 有两解.……………………………………6 分
设
22ln (1 ln ) 1( ) ,0 2, .1 2 1 2 2
x x x x x x x xg x x xxx
+ − + −= = −−
则 2
1(1 )( 2ln ) 1'( ) ,0 2, .(1 2 ) 2
x x xxg x x xx
−+
= −
令 1( ) 2ln ,0 2h x x xx= + ,则 22
1 2 2 1'( ) ,xhx x x x
−= − + =
故 min
1 1 1(0, ), '( ) 0, ( ,2), '( ) 0 ( ) ( ) ( ) 2 ln 4 02 2 2x h x x h x h x h x h = = −
故 11(0, ),( ,1), '( ) 0, (1,2), '( ) 022x g x x g x
从而 11(0, ),( ,1), ( ) , (1,2), ( )22x g x x g x递增 递减,
令 ( )=1 ln ,0 2t x x x x x+ − , '( ) ln ,t x x=
(0,1) '( ) 0, (1,2) '( ) 0x t x x t x 由于 时 时
第8页 共 8 页
min( ) ( ) (1) 0t x t x t = =
故 11(0, ), ( ) 0, ( ,2), ( ) 022x g x x g x ……………………………10 分
而 11( ,2) , ( ) (1) 0, ( )22x g x g x g x = → → −时 时,
故
22ln
12
x x x xm x
+−= − 在区间内 (0,2) 有两解 (2) 0gm ,
解得 2 4ln 2 03 m− .
………………………………………………………………12 分
(二)选考题:共 10 分。请考生在第 22、23 题中任选一题作答。如果多做,则按所做的
第一题计分。
22【解析】(1) 1 :C 22( 1) ( 4) 10xy− + − = , 2 :C 5x = .……………………………………5 分
(2)由(1) (5, )Pn,过 P 作曲线 1C 的两条切线,切点分别记为 ,MN,
由题, 90MPN,故 1 45MPC,
即 1
1
1
||2sin | | 2
MCMPC PC = ,即 22
11| | 2 | |PC MC ,…………………………………8 分
∴ 2 2 2(5 1) ( 4) 2 10 8 12 0n n n− + − − + ,
故 26n.………………………………………………………………………………10 分
(其他正确解答酌情给分)
23【解析】(1)由题:| 2 1| 2 | 1| 4xx− + + ,
当 1x − 时,1 2 2 2 4xx− − − ,∴ 5
4x − ,
当 11 2x− 时,1 2 2 2 4xx− + + ,无解,
当 1
2x 时, 2 1 2 2 4xx− + + ,∴ 3
4x ,
综上: ()fx的定义域为 53( , ) ( , )44− − + .……………………………………………5 分
(2)由题:| 2 1| 2 | 1|x x a− + + 恒成立.
∵| 2 1| 2 | 1| | 2 1| | 2 2 | | (2 1) (2 2) | 3x x x x x x− + + = − + + − − + = ,
故 3a . …………………………………………………………………………………10 分