2019-2020学年甘肃省兰州市联片办学高二上学期期中考试数学（文）试题（解析版） 14页

2019-2020 学年甘肃省兰州市联片办学高二上学期期中考试 数学（文）试题 一、单选题 1．下列数列中，既是递增数列又是无穷数列的是( ) A.－1，－2，－3，－4，… B.－1，－ 1 2 ，－ 1 3 ，－ 1 4 ，… C.－1，－2，－4，－8，… D.1， 2 ， 3 ， 4 ，…， 10 【答案】B 【解析】A，B，C 中的数列都是无穷数列，但是 A，C 中的数列是递减数列，故选 B. 2．下列不等式成立的是( ) A.若 2 2a b ，则 a b B.若 a b ，则 2 2a b C.若 a b ，则 2 2ac bc D.若 2 2ac bc ，则 a b 【答案】D 【解析】通过举反例进行排除，可排除 A，B，C，根据不等式的性质即可确定答案为 D. 【详解】 对于 A，当 1a   ， 0b  时，则不等式不成立， 对于 B，当 1a  ， 1b   时，则不等式不成立， 对于 C，当 0c = 时，则不等式不成立， 对于 D，根据不等式的基本性质可知 D 正确. 故选：D. 【点睛】 本题考查了不等式的基本性质，利用排除法是常用的手段，属基础题. 3．在△ ABC 中， 4, 30a A   ， 60B   ，则b 等于( ) A. 4 3 B.6 C. 3 D.9 【答案】A 【解析】由正弦定理进行求解即可. 【详解】 4a  ， 30A  ， 60B  ， 由正弦定理得 sin sin a b A B  ， 则 34sin 4 sin 60 2 4 31sin sin30 2 a Bb A       ， 故选：A. 【点睛】 本题主要考查正弦定理的应用，利用正弦定理是解决本题的关键，属基础题. 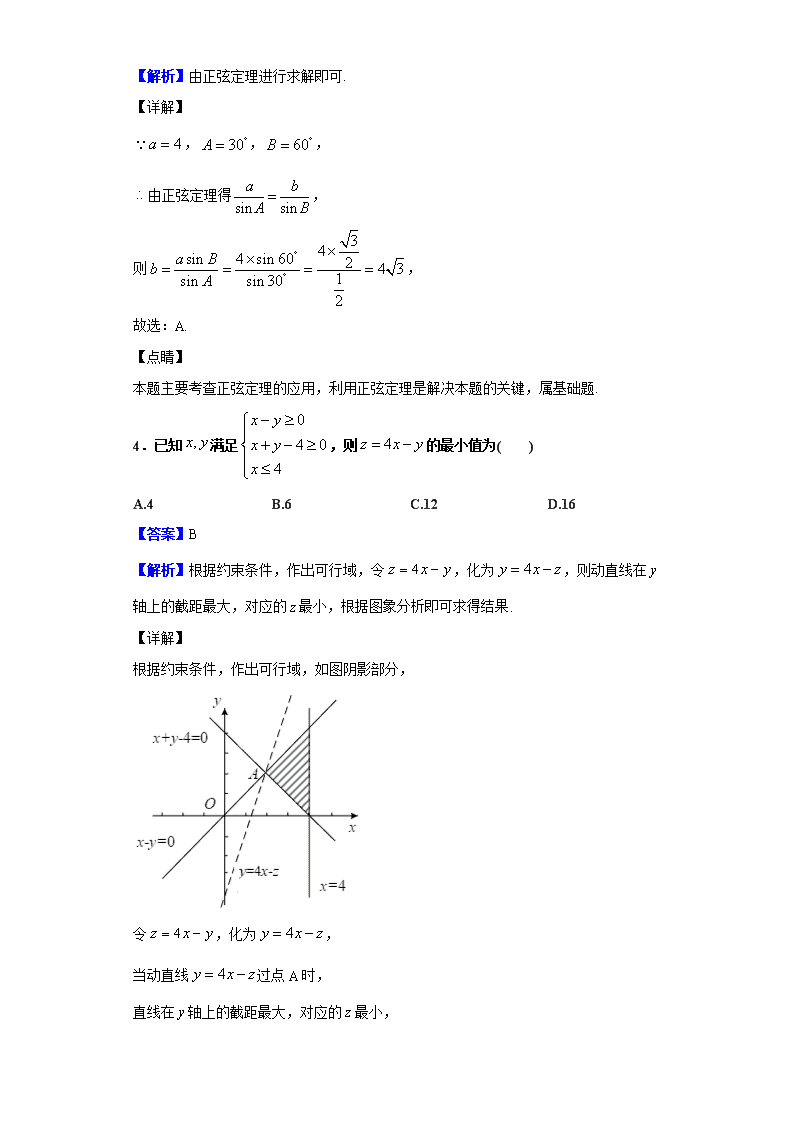4．已知 ,x y 满足 0 4 0 4 x y x y x         ，则 4z x y  的最小值为( ) A.4 B.6 C.12 D.16 【答案】B 【解析】根据约束条件，作出可行域，令 4z x y  ，化为 4y x z  ，则动直线在 y 轴上的截距最大，对应的 z 最小，根据图象分析即可求得结果. 【详解】 根据约束条件，作出可行域，如图阴影部分， 令 4z x y  ，化为 4y x z  ， 当动直线 4y x z  过点 A 时， 直线在 y 轴上的截距最大，对应的 z 最小， 联立 4 0 0 x y x y       ，解得 2 2 x y    ，则 (2,2)A ， 则 z 的最小值为 min 4 2 2 6z     . 故选：B. 【点睛】 本题考查线性规划问题，正确做出可行域是解题的关键，属基础题. 5．在等差数列{an}中，若 a1，a4 是方程 x2-x-6=0 的两根，则 a2+a3 的值为（ ） A．6 B．-6 C．-1 D．1 【答案】D 【解析】试题分析：由韦达定理得 ，再由等差数列下标和的性质可知 ． 【考点】等差数列下标和的性质． 6．设△ ABC 的内角 , ,A B C 所对的边分别为 , ,a b c ，若 cos cos sinb C c B a A  ， 则△ ABC 的形状为（ ） A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰直角三角形 【答案】C 【解析】首先由正弦定理可得：sinBcosC+sinCcosB= sin2A，接下来利用两角和的正弦公 式与诱导公式对 sinBcosC+sinCcosB 进行变形可得 sinA，由上步可得 sinA=sinAsinA，然 后解出满足条件的 A 的值，即可判断出该三角形的形状. 【详解】 ∵bcosC+ccosB=asinA， ∴sinBcosC+sinCcosB=sin2A. ∵sinBcosC+sinCcosB=sin(B+C)=sinA， ∴sinA=sin2A. ∵sinA≠0， ∴sinA=1. ∵0＜A＜π， ∴A= 2  . 故△ABC 为直角三角形. 故选：C 【点睛】 本题是一道判断三角形形状的题目，考查了利用正弦定理解三角形，利用正弦定理进行 “边化角”是本题的关键，属基础题. 7．设等差数列{ }na 的前 n 项和为 nS ，若 1a 11  ， 4 6 6a a   ，则当 nS 取最小值 时， n 等于( ) A.6 B.7 C.8 D.9 【答案】A 【解析】设数列{ }na 的公差为 d，根据题意，可列方程求解 d，然后得到 nS 的求和公式， 从而利用二次函数的求最值的方法即可求得结果. 【详解】 设数列{ }na 的公差为 d， 因为 1 11a   ，所以 4 6 12 8 22 8 6a a a d d        ，解得 2d  ， 因此 2 2 1 ( 1) 11 ( 1) 12 ( 6) 362n n nS na d n n n n n n            ， 故当 6n  时， nS 取最小值为 36 . 故选：A. 【点睛】 本题主要考查等差数列的通项公式的计算和前 n 项和的最值问题，要求熟记公式，认真 计算，属基础题. 8．已知△ ABC 的两边长分别为 2,3，这两边的夹角的余弦值为 1 3 ，则△ ABC 的外接 圆的直径为（ ） A. 9 2 2 B. 9 2 4 C. 9 2 6 D.8 2 【答案】B 【解析】利用同角三角函数的基本关系求得三角形边长分别为 2、3 的夹角的正弦值为 2 2 3 ，由余弦定理可求第三边的长，根据正弦定理即可求得外接圆的直径. 【详解】 ABC△ 的两边长分别为 2、3，其夹角的余弦为 1 3 ，故其夹角的正弦值为 1 2 21 9 3   ， 由余弦定理可得第三边的长为： 2 2 12 3 2 2 3 33       ， 则利用正弦定理可得： ABC△ 的外接圆的直径为 3 9 2 42 2 3  . 故选：B. 【点睛】 本题主要考查同角三角函数的基本关系，三角形的面积公式以及正弦定理与余弦定理的 应用，注意认真计算，仔细检查，属基础题. 9．已知等差数列 na 中， nS 是 na 的前 n 项和，且 3 30S  ， 6 100S  ，则 9S 的值 为 ( ) A.260 B.130 C.170 D.210 【答案】D 【解析】由题意结合等差数列的性质整理计算即可求得最终结果. 【详解】 由题意可得 3S ， 6 3S S ， 9 6S S ，成等差数列， 故    6 3 3 9 62 S S S S S    ， 代入数据可得   92 100 30 30 100S    ， 解之可得 9 210S  本题选择 D 选项. 【点睛】 本题主要考查等差数列前 n 项和的性质及其应用等知识，意在考查学生的转化能力和计 算求解能力. 10．在各项均为正数的等比数列{ }na 中，若 2 4 9a a  ，则 1 1 1 2 3 3 log loga a 1 3 3 log a  1 4 1 5 3 3 log loga a 的值为（ ） A.6 B.5 C.-6 D.-5 【答案】D 【解析】据等比数列的性质可知 2 2 4 1 5 3 9a a a a a    ，再利用对数的运算性质即可 得到答案. 【详解】  各项均为正数的等比数列 na 中， 2 2 4 1 5 3 9a a a a a    ， 3 3a  ， 1 1 1 2 1 3 1 4 1 5 3 3 3 3 3 log log log loglog a a a a a        1 1 5 1 2 4 1 3 1 3 3 3 3 3 log log log 5log 5a a a a a a      . 故选：D. 【点睛】 本题主要考查了对数的运算和等比数列的性质，即若 , , ,m n p q  ，且 m n p q   ， 则 m n p qa a a a ，属基础题. 11．在△ ABC 中， , ,a b c 分别为角 , ,A B C 的对边，已知 60A   ， 1b  ，面积 3S  ， 则 sin sin sin a b c A B C     等于( ) A. 2 39 3 B. 8 3 3 C. 26 3 3 D. 39 26 【答案】A 【解析】由正弦定理可得 sin sin sin sin a b c a A B C A     ，根据三角形面积公式可求 c， 然后利用余弦定理求出 a，从而可求得结果. 【详解】 由正弦定理， 2sin sin sin a b c RA B C    （ R 为三角形外接圆的半径）， 所以 2 sin 2 sin 2 sin 2sin sin sin sin sin sin sin a b c R A R B R C aRA B C A B C A          . 因为 1 1sin 1 sin 60 32 2ABCS bc A c       ，所以 4c  ， 根据余弦定理， 2 2 2 2 22 cos 1 4 2 1 4 cos60 13a b c bc A           ， 解得 13a  ，所以 13 2 39 sin sin sin sin sin 60 3 a b c a A B C A        . 故选：A. 【点睛】 本题考查正弦定理和余弦定理的应用，也考查了三角形的面积公式，要求熟练掌握定理， 准确计算，属中档题. 12．已知△ ABC 中，三个内角 , ,A B C 的对边分别为 , ,a b c ，若△ ABC 的面积为 S ， 且 2 22 ( )S a b c   ，则 tanC 等于( ) A. 3 4 B. 4 3 C. 4 3  D. 3 4  【答案】C 【解析】根据面积公式，将 2 22 ( )S a b c   变形为 2 2 2sin 2ab C ab a b c    ，又 2 2 2 cos 2 a b cC ab   ，两式结合化简可得 sincos 1 2 CC   ，再利用二倍角公式化简得 到 tan 22 C  ，从而可求得 tanC . 【详解】 由 2 22 ( )S a b c   得 2 2 22 2S a b ab c    ， 即 2 2 212 sin 22 ab C a b ab c     ， 则 2 2 2sin 2ab C ab a b c    ， 又因为 2 2 2 sin 2 sincos 12 2 2 a b c ab C ab CC ab ab       ， 所以 sincos 1 2 CC   ， 即 22cos sin cos2 2 2 C C C ，由 (0, )C  ， 所以 tan 22 C  ，即 2 2 2tan 2 2 42tan 1 2 31 tan 2 C C C     . 故选：C. 【点睛】 本题考查三角形面积公式和余弦定理的应用，也考查了三角函数的二倍角公式，熟练掌 握定理和公式是解题的关键，属中档题. 二、填空题 13．设 7 10a   ， 3 14b   ，则 a 与b 的大小关系是________． 【答案】 a b 【解析】首先分别求出 7 10 和 3 14 平方各是多少，然后判断出 7 10 和 3 14 的平方的大小关系，即可判断出 7 10 和 3 14 的大小关系. 【详解】 2( 7 10) 7 10 2 70 17 2 70      ， 2( 3 14) 3 14 2 42 17 2 42      ， 17 2 70 17 2 42   ， 2 2( 7 10) ( 3 14)    ，且 7 10 0  ， 3 14 0  ， 7 10 3 14    . 故答案为： a b . 【点睛】 本题主要考查了实数大小比较的方法，要熟练掌握不等式的基本性质，解答本题的关键 是判断出两个数的平方的大小关系，属基础题. 14．在△ ABC 中，设角 , ,A B C 的对边分别为 , ,a b c ，如果 : : 3: 2: 4a b c  ，那么 cosC  ____． 【答案】 1 4  【解析】由已知的 : :a b c 的比值设出 a，b 及 c，然后利用余弦定理表示出 cosC，把设 出的 a，b 及 c 代入，化简可得 cosC 的值. 【详解】 因为 : : 3: 2: 4a b c  ，所以设 3a k ， 2b k ， 4c k ， 则根据余弦定理得： 2 2 2 2 2 2 2 9 4 16 1cos 2 12 4 a b c k k kC ab k        . 故答案为： 1 4  . 【点睛】 本题考查了余弦定理，以及比例的性质，熟练掌握余弦定理是解本题的关键，属基础题. 15．已知数列{ }na 的前 n 项和 3 2n nS   ,则 na  ________ 【答案】 1 5, 1 2 3 , 2n n n     【解析】分析题意知，由数列{an}的前 n 项和为 3 2n nS   可得 a1=S1=5，接下来分析 n≥2 时，由公式 an=Sn-Sn-1 不难确定数列{an}的通项公式. 【详解】 当 n=1 时，a1=S1=5， 当 n≥2 时， 1 1 1 3 2 (3 2) 2 3n n n n n na S S           ， 显然，a1 不满足上式， 综上可得 an= 1 5, 1 2 3 , 2n n n     . 故答案为： 1 5, 1 2 3 , 2n n n     . 【点睛】 本题是一道求解数列通项的题目，熟练掌握 an 与 Sn 的关系求数列的通项是解题的关键， 属基础题. 16．若对于任意的 [ 1,2]x   ， 2 2 3 2 0x x m    恒成立，则实数 m 的取值范围是 ________ 【答案】 1m £ 【解析】将不等式分离参数，得到新的不等式，构造函数并求出新函数在 x∈[-1，2]的 最小值即可求得结果． 【详解】 要使 2 2 3 2 0x x m    恒成立，即使得 2 2 3 2 x xm   在 x∈[-1，2]恒成立. 令 2 2 3 2 x xt   ，当 1x   时，t 取得最小值 1，则实数 m 的取值范围是：m≤1. 故答案为：m≤1. 【点睛】 本题考查不等式恒成立问题，二次函数最值问题，将不等式恒成立问题转化为求函数的 最值问题是常用手段，属中档题. 三、解答题 17．已知不等式 2 3 2 0ax x   （1）若 2a   ，求上述不等式的解集； （2）不等式 2 3 2 0ax x   的解集为{ | 1x x  或 }x b ，求 ,a b 的值． 【答案】（1） 1( 2, )2  ；（2） 1a  ， 2b  . 【解析】（1）对不等式进行变形，结合因式分解即可求得不等式的解集；（2）根据一元 二次不等式的解与一元二次方程的根的关系可知方程 2 3 2 0ax x   两个根，再利用 韦达定理即可求出 a 和 b. 【详解】 （1）依题意， 22 3 2 0x x    ，即 22 3 2 0x x   ，即 (2 1)( 2) 0x x   ， 解得， 12 2x   ，则不等式的解集为 1( 2, )2  ； （2）设方程 2 3 2 0ax x   ，依题意，该方程的根为 1x  或 x b ， 由韦达定理可得， 1 2 2x x ba   ， 1 2 3 1x x ba     ， 联立以上两式，可得 1a  ， 2b  . 【点睛】 本题考查一元二次不等式的求解方法，以及一元二次不等式的解与一元二次方程的根的 关系，注意仔细审题，认真计算，属中档题. 18．在 ABC 中， 45 , 10B AC   ，且 2 5cos 5C  . （1）求 BC 边长； （2）求 AB 边上中线 CD 的长. 【答案】（1）3 2 ；（2） 13 . 【解析】（1）利用同角的三角函数关系，可以求出 sin C 的值，利用三角形内角和定理， 二角和的正弦公式可以求出 sin A ，最后利用正弦定理求出 BC 长； （2）利用余弦定理可以求出 AB 的长，进而可以求出 BD 的长，然后在 BCD 中，再 利用余弦定理求出 AB 边上中线CD 的长. 【详解】 （1） 2 5(0, ) sin 1 cos 5C C C     ， 3 10sin sin( ) sin cos cos sin 10A B C B C B C        ，由正弦定理可知中： sin 3 2;sin sin sin BC AC AC ABCA B B     （2）由余弦定理可知： 2 2 2 52 cos 10 18 2 10 3 2 25AB AC BC AC BC C            ， D 是 AB 的中点，故 1BD  ，在 CBD 中，由余弦定理可知： 2 2 22 cos 18 1 2 3 2 1 13.2CD BC BD BC BD B            【点睛】 本题考查了正弦定理、余弦定理、同角的三角函数关系、以及三角形内角和定理，考查 了数学运算能力. 19．已知等比数列 na 中， 1 2a  ，且 4 16a  . （1）求数列 na 的通项公式； （2）求数列 nn a 的前 n 项和 nT . 【答案】（1） 2n na  ；（2）   11 2 2nn   . 【解析】试题分析：（1）根据题意列出关于首项 1a ，公比 q 的方程组，解得 1a 、q的 值，即可求数列 na 的通项公式；（2）由（1）可得 2n nna n  ，利用错位相减法即可 得到数列的和. 试题解析：（1） 3 3 4 116 16, 8, 2a a q q q      ，即 2n na  . (2) 2 32 , 2 2 2 3 2 ... 2n n n nna n S n           ， ① （i）当 1n  时， 1 2S  ；（ii）当 2n  时， 2 3 12 2 2 2 ... 2 2n nS       ， ② ①-②得，  2 1 12 2 2 2 2 ... 2 2 21 2 n n n n nS n n            ，整理得   11 2 2n nS n     ，由（i）(ii)得   11 2 2n nS n     . 【 方法点睛】本题主要考查等比数列的通项与求和公式以及错位相减法求数列的的前 n 项和，属于中档题.一般地，如果数列 na 是等差数列， nb 是等比数列，求数列  n na b 的前 n 项和时，可采用“错位相减法”求和，一般是和式两边同乘以等比数列  nb 的公比，然后作差求解, 在写出“ nS ” 与“ nqS ” 的表达式时应特别注意将两式“错 项对齐”以便下一步准确写出“ n nS qS ”的表达式. 20．在△ ABC 中，角 , ,A B C 所对的边分别为 , ,a b c ，且 cos cos 2 cosa C c A b A  . （1）求角 A 的大小；（2）若 3, 2a c  ，求△ ABC 的面积. 【答案】（1） 3A  ；（2） 3 2ABCS  【解析】（1）利用正弦定理化简已知条件，通过两角和与差的三角函数化简求解即可； （2）通过余弦定理求出 b，然后求解三角形的面积. 【详解】 （1）因为 cos ccos 2 cosa C A b A  ， 由正弦定理可得：sin cos sin cos 2sin cosA C C A B A  ， 所以sin( ) 2sin cosA C B A  ，即sin 2sin cosB B A ， 由sin 0B  ，则 1cos 2A  ， 由于 0 A   ，故 3A  ； （2）由余弦定理得， 2 2 2( 3) 2 2 2 cos 3AC AC       ，所以 1AC  ， 故 1 32 1 sin2 3 2ABCS      . 【点睛】 本题考查正弦定理与余弦定理的应用，考查计算能力，注意认真计算，书写规范，属中 档题. 21．已知在等比数列{an}中， 2a ＝2，， 4 5a a ＝128，数列{bn}满足 b1＝1，b2＝2，且 { 1 2n nb a }为等差数列． （1）求数列{an}和{bn}的通项公式； （2）求数列{bn}的前 n 项和 【答案】（1） 1 232 ; 2 ,2 1 2n n n na b n n    （ ＝，， ）；（2） 2 13 3 124 4 2 n nT n n     . 【解析】(1)根据等比数列的性质得到 7a ＝64， 2a ＝2，进而求出公比，得到数列{an}的 通项，再由等差数列的公式得到结果；（2）根据第一问得到通项，分组求和即可. 【详解】 （1）设等比数列{an}的公比为 q． 由等比数列的性质得 a4a5＝ 2 7a a ＝128，又 2a ＝2，所以 7a ＝64． 所以公比 7 55 2 64 22 aq a    ． 所以数列{an}的通项公式为 an＝a2qn－2＝2×2n－2＝2n－1． 设等差数列{ 1 2n nb a }的公差为 d． 由题意得，公差 2 2 1 1 1 1 1 1 32 2 1 12 2 2 2 2d b a b a                                ， 所以等差数列{ 1 2n nb a }的通项公式为    1 1 1 1 3 3 31 12 2 2 2 2n nb a b a n d n n             ． 所以数列{bn}的通项公式为 1 23 1 3 1 32 22 2 2 2 2 n n n nb n a n n        （n＝1，2，…）． （2）设数列{bn}的前 n 项和为 Tn． 由（1）知， 23 22 n nb n   （n＝1，2，…）． 记数列{ 3 2 n }的前 n 项和为 A，数列{2n－2}的前 n 项和为 B，则   3 3 32 2 12 4 n n A n n       ，   1 1 1 2 12 21 2 2 n nB      ． 所以数列{bn}的前 n 项和为   1 2 13 1 3 3 11 2 24 2 4 4 2 n n nT A B n n n n           ． 【点睛】 这个题目考查了数列的通项公式的求法，以及数列求和的应用，常见的数列求和的方法 有：分组求和，错位相减求和，倒序相加等. 22．已知等比数列{ }na 的首项为 1，公比 1q  ， nS 为其前 n 项和， 1 2 3, ,a a a 分别为某 等差数列的第一、第二、第四项. （1）求 na 和 nS ； （2）设 2 1logn nb a  ，数列 2 1{ } n nb b  的前 n 项和为 nT ，求证： 3 4nT  . 【答案】（1） 12n na -= ， 2 1n nS   ；（2）证明见解析 【解析】（1）由题意可得  3 2 2 12a a a a   ，结合等比数列的通项公式得到关于 q 的方程，解方程可求 q，进而利用等比数列的通项公式可求 na 和 nS ；（2）由（1）可知， 2 1logn nb a n  ，代入 2 1 1 1 1 1 ( 2) 2 2n nb b n n n n        ，利用裂项求和方法即可 求解 nT ，从而可证明结论. 【详解】 （1） 1 2 3, ,a a a 分别为某等差数列的第一、第二、第四项，  3 2 2 12a a a a    ， 2 1 1 1 12 2a q a q a q a    ， 1 1a  ， 2 3 2 0q q    ，且 1q  ， 2q  ， 12n na - = ， 1 2 2 11 2 n n nS    ； （2）由（1）可知， 2 1logn nb a n  ， 2 1 1 1 1 1 ( 2) 2 2n nb b n n n n         ， 1 1 1 1 1 112 3 2 4 2nT n n           1 1 1 112 2 1 2n n         3 1 1 1 3 4 2 1 2 4n n         . 【点睛】 本题主要考查了等差数列的性质及等比数列的通项公式的应用，以及数列的裂项求和方 法的应用，要求计算认真，书写规范，属中档题.