- 1.02 MB
- 2024-01-13 发布
宁夏六盘山高级中学2017届高三第三次模拟考试
数学(文)试题
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知,,则( )
A. B. C. D.
2.已知是虚数单位,若为纯虚数,则( )
A. -1 B.1 C. 0 D.2
3.某4名同学(其中2男2女)报考了2017年高考英语口语考试,若有三人通过了考试,则女生甲通过考试的概率是( )
A. B. C. D.
4.直线与圆的位置关系是( )
A. 相离 B.相交 C. 相切 D.无法判定
5.若是第四象限角,且,则( )
A. B. C. D.
6.已知数列是等差数列,且,,则( )
A.12 B. 24 C. 16 D.32
7.设,则的零点位于区间( )
A. B. C. D.
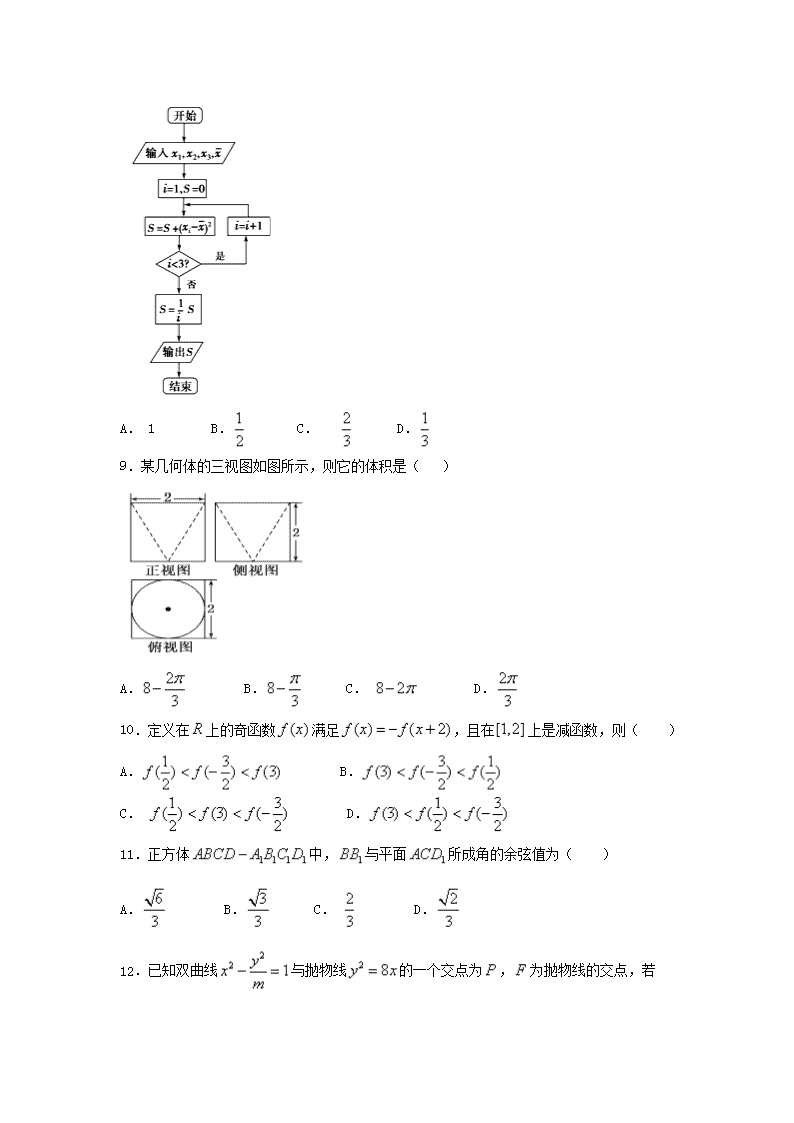
8.若执行如图所示的框图,输入,,,,则输出的数等于( )
A. 1 B. C. D.
9.某几何体的三视图如图所示,则它的体积是( )
A. B. C. D.
10.定义在上的奇函数满足,且在上是减函数,则( )
A. B.
C. D.
11.正方体中,与平面所成角的余弦值为( )
A. B. C. D.
12.已知双曲线与抛物线的一个交点为,为抛物线的交点,若
,则双曲线的离心率为( )
A. B. 4 C. D.2
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知向量满足,,,则 .
14.等比数列的前项和为,若,则公比 .
15.函数在处有极值,则曲线在原点处的切线方程为 .
16.某工厂有两种配件生产甲、乙两种产品,每生产一件甲产品使用4个配件,耗时1,每生产一件乙产品使用4个配件,耗时2,该厂每天最多可从配件厂获得24个配件和16个配件,每天生产总耗时不超过8,若生产一件甲产品获利3万元,生产一件乙产品获利4万元,则通过恰当的生产安排,该工厂每天可获得的最大利润为 万元.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. ,内角所对的边分别是,且.
(1)求角的大小;
(2)若,,求.
18. 如图所示,矩形中,,,沿对角线把折起,使点在平面上的射影落在上.
(1)求证:平面平面;
(2)求三棱锥的体积.
19. 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了人,得到如下的统计表和频率分布直方图.
(1)写出其中及和的值;
(2)若从第1,2,3,组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求抽取的2人年龄都在的概率.
20. 设椭圆的左焦点为,离心率为,过点且与轴垂直的直线被椭圆截得的线段长为.
(1)求椭圆的方程;
(2)设分别为椭圆的左、右顶点,过点且斜率为的直线与椭圆交于两点,若,求的值.
21. 设为实数,函数.
(1)求的单调区间及极值;
(2)求证:当且时,.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
在直角坐标系中,圆的参数方程为(为参数),圆的方程为(为参数),以为极点,轴正半轴为极轴建立极坐标系.
(1)求圆、圆的极坐标方程;
(2)射线同时与圆交于两点,与圆交于两点,求的最大值.
23.选修4-5:不等式选讲
设函数,不等式的解集为.
(1)求;
(2)当时,证明:.
试卷答案
一、选择题
1-5: BADCC 6-10: ABCAB 11、12:AD
二、填空题
13. 3 14. -2 15. 16.22
三、解答题
17. (1)∵
∴,由正弦定理得:,
即,
∵,∴,∴,.
(2) 由(1) 知,
∵,
∴,解得.
∴,
∴.
18.解:
(1)∵AE⊥平面BCD,∴AE⊥CD.
又BC⊥CD,且AE∩BC=E,
∴CD⊥平面ABC.
又CD⊂平面ACD,
∴平面ACD⊥平面ABC.
(2)由(1)知,CD⊥平面ABC,
又AB⊂平面ABC,∴CD⊥AB.
又∵AB⊥AD,CD∩AD=D,
∴AB⊥平面ACD.
∴VA-BCD=VB-ACD=·S△ACD·AB.
又∵在△ACD中,AC⊥CD,AD=BC=4,AB=CD=3 ,
∴AC=.
∴VA-BCD=
19.(Ⅰ)由表可知第3组,第4组 的人数分别为,,再根据直方图可知第1组、第2组的人数也为人,且抽样总人数.
所以第5组的人数为,
且 ,,,
,
(Ⅱ)因为第1,2,3组喜欢地方戏曲的人数比,
那么用分层抽样的方法从这三组中抽取6人
第1组应抽取1人,
第2组应抽取2人,
第3组应抽取3人.
(Ⅲ) 由(Ⅱ)第3组抽到3人,记为第1组和第2组3人记为
从这六人中随机抽取2人,所有可能结果共有15种,分别为
所抽取2人都在第3组的结果有3人,故所求的概率为
20.解:(1)设F(-c,0),由,知.过点F且与x轴垂直的直线为x=-c,
代入椭圆方程有,解得.
于是,解得.又a2-c2=b2,从而,c=1,所以椭圆的方程为.
(2)设点C(x1,y1),D(x2,y2),由F(-1,0)得直线CD的方程为y=k(x+1).
由方程组消去y,整理得(2+3k2)x2+6k2x+3k2-6=0.
由根与系数的关系得x1+x2=,x1x2=.
因为A(-,0),B(,0),所以=(x1+,y1)·(-x2,-y2)+(x2+,y2)·(-x1,-y1)
=6-2x1x2-2y1y2=6-2x1x2-2k2(x1+1)(x2+1)
=6-(2+2k2)x1x2-2k2(x1+x2)-2k2
=6+.
由已知得6+=8,解得k=±.
21.(1):
∵
∴,,令,得.
当,,单调递减,
当,,单调递增,
故的单调递增区间是,减区间为,
是的极小值点,极小值为,无极大值.
(2)
设,
于是,
由(1)知,当时,的最小值
于是对任意,都有
所以在内单调递增.
所以当时,对任意,都有,
而,所以对任意的,,
即,故.
22.(1)
(2) ,
的极坐标为,
所以
∵,∴当,即时,取得最大值4.
23.(1)由题意
当时,得;
当时,得;
当时,得,所以.
(2) ,即,,
∴
∴,即