- 1.48 MB
- 2024-01-08 发布
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符
合题目要求的。
1.已知复数 (1 )(3 )z i i (i 为虚数单位),则 z 的虚部为( )
A.2 B. 2i C.4 D. 4i
解:易知复数 (1 )(3 ) 4 2z i i i ,故 z 的虚部为 2,选 A.
2.设集合 1 1M x x , 1N x x ,则 M N =( )
A. 1x x B. 1x x 或 2x C. 0 1x x D. 0x x
解:由 1 1 2 0M x x x x x 或 且 1N x x 得 0M n x x ,选 D.
3.已知函数 ( )f x 是定义在 R 上的奇函数,当 ( ,0)x 时, 3 2( ) 2f x x x ,则 (3)f =( )
A.9 B.-9 C.45 D.-45
解:由 (3) ( 3) ( 27 18) 45f f ,选 C.
4. 若 10,1 bca ,则下列不等式不正确的是( )
A. 2019 2019log loga b B.log logc ba a
C. bc abcabc D. bc acaaca )()(
解:由 1,0 1a c b 有 , 0c ba a a c ,故有 ( ) ( )c ba c a a c a ,选 D.
5. 已知函数 2
1( ) 4 4f x x x
,则 ( )f x 的大致图象是( )
A B C D
解:易知当 0 1x 时, ( ) 0f x ; 0 1x x 或 时, ( ) 0f x ,可排除 A、C,又可由 1 1
3 2( ) ( )f f
排除 D,故选 B.
6. 甲、乙两名同学在 6 次数学考试中,所得成绩用茎叶图表示如下,若甲、乙两人这 6 次考试的平
均成绩分别用 x甲 、 x乙 表示,则下列结论正确的是( )
A. x x甲 乙 ,且甲成绩比乙成绩稳定
B. x x甲 乙 ,且乙成绩比甲成绩稳定
C. x x甲 乙 ,且甲成绩比乙成绩稳定
D. x x甲 乙 ,且乙成绩比甲成绩稳定
解:根据茎叶图中数据可求得 82x 甲 、 83x 乙 , 2 74
3S 甲 , 2 164
3S 乙 故选 C.
安徽六校教育研究会 2020 届高三第一次素质测试
文科数学参考答案
1
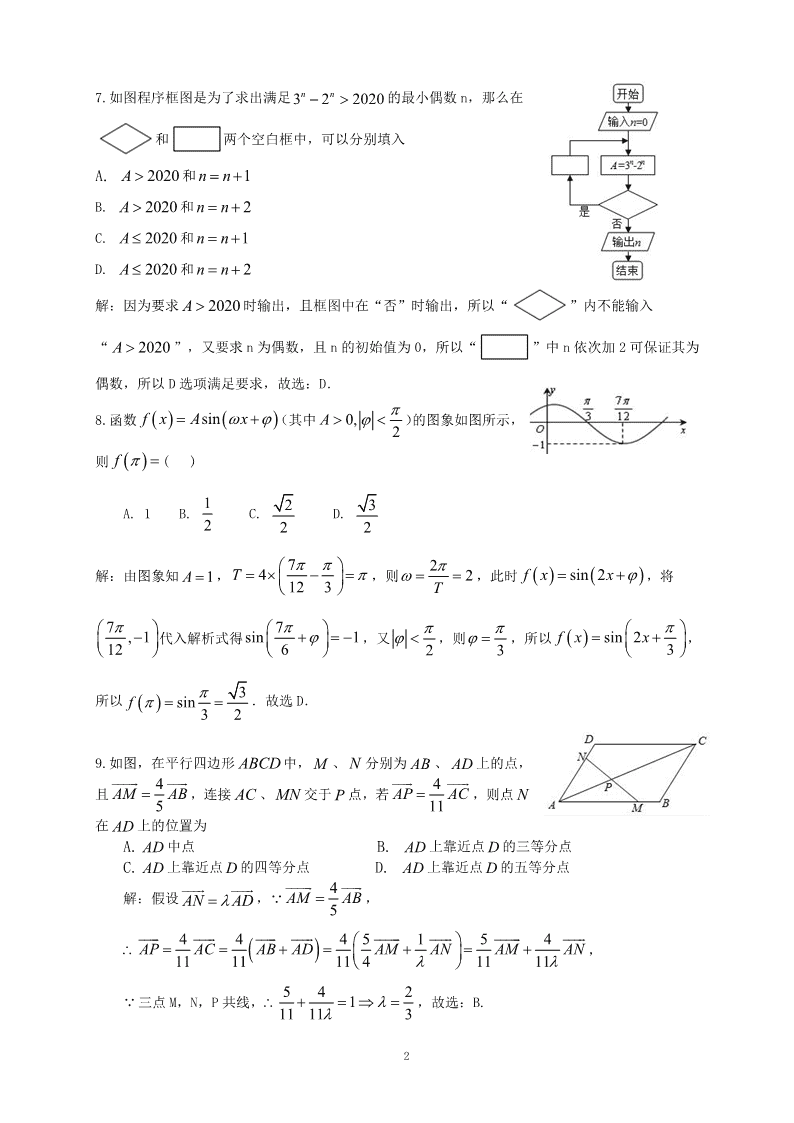
7.如图程序框图是为了求出满足3 2 2020n n 的最小偶数 n,那么在
和 两个空白框中,可以分别填入
A. 2020A 和 1n n
B. 2020A 和 2n n
C. 2020A 和 1n n
D. 2020A 和 2n n
解:因为要求 2020A 时输出,且框图中在“否”时输出,所以“ ”内不能输入
“ 2020A ”,又要求 n 为偶数,且 n 的初始值为 0,所以“ ”中 n 依次加 2 可保证其为
偶数,所以 D 选项满足要求,故选:D.
8.函数 sinf x A x (其中 0, 2A )的图象如图所示,
则 f ( )
A. 1 B. 1
2
C. 2
2
D. 3
2
解:由图象知 1A , 74 12 3T
,则 2 2T
,此时 sin 2f x x ,将
7 , 112
代入解析式得 7sin 16
,又
2
,则
3
,所以 sin 2 3f x x
,
所以 3sin 3 2f .故选 D.
9.如图,在平行四边形 ABCD 中, M 、 N 分别为 AB 、 AD 上的点,
且 4
5AM AB
,连接 AC 、 MN 交于 P 点,若 4
11AP AC
,则点 N
在 AD 上的位置为
A. AD 中点 B. AD 上靠近点 D 的三等分点
C. AD 上靠近点 D 的四等分点 D. AD 上靠近点 D 的五等分点
解:假设 AN AD
, 4
5AM AB
,
4 4 4 5 1 5 4
11 11 11 4 11 11AP AC AB AD AM AN AM AN
,
三点 M,N,P 共线, 5 4 2111 11 3 ,故选:B.
2
10.已知椭圆
2 2
2 2: 1( 0)x yC a ba b 的右焦点为 F ,短轴的一个端点为 P ,直线 : 4 3 0l x y
与椭圆相交于 A 、 B 两点.若| | | | 6AF BF ,点 P 到直线l 的距离不小于 6
5
,则椭圆离心率的取
值范围为( )
A. 9(0, ]5
B. 3(0, ]2
C. 5(0, ]3
D. 1 3( , ]3 2
解:设椭圆的左焦点为 F , P 为短轴的上端点,连接 ,AF BF ,如下图所示:
由椭圆的对称性可知, ,A B 关于原点对称,则OA OB ,
又OF OF ,四边形 AFBF 为平行四边形, AF BF
又 2 6AF BF BF BF a ,解得: 3a ,
点 P 到直线l 距离: 3 6
5 5
bd ,解得: 2b ,即 2 2 29 2a c c ,
0 5c ,
50, 3
ce a
。本题正确选项:C .
11.某罐头加工厂库存芒果 m kg ,今年又购进 n kg 新芒果后,欲将芒果总量的三分之一用于加
工为芒果罐头。被加工为罐头的新芒果最多为 1f kg ,最少为 2f kg ,则下列坐标图最能准确描
述 1f 、 2f 分别与 n 的关系的是( )
解:要使得被加工为罐头的新芒果最少,尽量使用库存芒果,即当 m n m,n 2m3
时,此时 2f 0 ,
当 n 2m 时, 2
n m n 2mf m3 3
,对照图象舍去 B,D;
要使得被加工为罐头的新芒果最多,则尽量使用新芒果,即当
m n mn,n3 2
时 1
m nf 3
,当 m n mn,n3 2
时 1f n ,因为 m 2m2 ,所以选 C.
3
12.如图, 1 2F F、 是双曲线
2 2
2 2 1: 0, 0C ax y
a b b 的左、右焦点,过 2F 的直线与双曲线C 交
于 A B、 两点.若 1 1: : 3: 4 :5AB BF AF .则双曲线的渐近线方程为( )
A. xy 32 B. xy 22 C. xy 3 D. xy 2
解:设 2 , 3AF t AB x ,则 1 14 , 5BF AFx x ,根据双曲线的定义
得: 1 2 2 1 2AF AF BF BF a ,即 5 3 4 2x t x t x a ,解得:
3 , t x a x
∵ 1 1: : 3: 4 :5AB BF AF ,得 1ABF 是以 B 为直角的直角三角形.
∴ 1
1
| | 3cos 5
ABBAF AF ,可得 2 1
3cos 5F AF ,
2 1F AF 中, 2 2 2
1 2 1 2 1 2 2 1| | | | | | 2 co| s| | |F F AF AF AF AF F AF
2 2 2325 9 2 5 3 525( )x x x x x ,可得 1 2| | 2 13F F x ,因
此,该双曲线的离心率 2 2 13 132 2
c xe a x ,所以渐近线为 xy 32 .
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.若函数 ( ) ln 2f x x ax 的图象存在与直线 2 0x y 垂直的切线,则实数 a 的取值范围
是 .
解 : 由 ( ) ln 2f x x ax 有 ' 1( ) 2f x ax , 则 由 题 意 即 1 12 2ax 在 (0, ) 上 有 解 , 由
1 1 12 ( , )2 2a x 有实数 a 的取值范围是 1( , )4 .
14.设等 差数列 na 的公 差 d 不为 0, 1 16a d ,若 ka 是 1a 与 2ka 的等 比中项 ,则 k 等
于 .
解:易知 216 ( 1) ( 15) , 16 (2 1) (2 15)k ka d k d k d a d k d k d ,由 ka 是 1a 与 2ka 的
等比中项可得 216 (2 15) ( 15)a k d k d 化简 2 2 15 0k k 得,有唯一正整数解为 5.
15.将函数 ( ) 4cos 2f x x
和直线 ( ) 1g x x 的所有交点从左到右依次记为 1A , 2A ,…, 5A ,
若 P 点坐标为 (0, 3) ,则 1 2 5...PA PA PA
_____.
解:
4
函数 ( ) 4cos 2f x x
与 ( ) 1g x x 的所有交点从左往右依次记为 1A 、 2A 、 3A 、 4A 和 5A ,且 1A
和 5A , 2A 和 4A ,都关于点 3A 对称,如图所示;则
1 2 5 3... 5 5(1, 3)= 5 3)PA PA PA PA
( ,-5 ,所以 1 2 5...PA PA PA
10.
16.如图,在棱长为 1 的正方体 1 1 1 1ABCD A B C D 中,点 M 是 AD 的中点,
动点 P 在底面 ABCD 内(不包括边界),若 1B P 平面 1A BM ,则 1C P 的最小
值是_____.
解:如图,在 1 1A D 上取中点Q ,在 BC 上取中点 N ,连接 1 1, , ,DN NB B Q QD
/ /DN BM , 1/ /DQ A M 且 DN DQ D , 1BM A M M ,
平面 1 / /B QDN 平面 1A BM ,则动点 P 的轨迹是 DN (不含 ,D N 两点),
又 1CC 平面 ABCD ,则当CP DN 时, 1C P 取得最小值,
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分 10 分)设等比数列 na 满足 1 3 20a a , 2 4 10a a ,
(Ⅰ)令 1 2 3n nT a a a a ,求 nT 的最大值;
(Ⅱ)令 2logn nb a ,求数列 n na b 的前 n 项和 nS .
解:(Ⅰ)由题 2 4
1 2
1
2
a aq a a
,又由 2
1 1 20a a q 可得 1 16a ,
故
1
5 *116 2 ( )2
n
n
na n N
…………………………………………………2 分
则1 4n 时 1, 5na n 时 1na , 6n 时,0 1na ,
则 4n 或 5 时, 1 2 3n nT a a a a 最大为16 8 4 2 1024 . ………………5 分
5
(Ⅱ)令 2log 5n nb a n ,则 5(5 ) 2 n
n na b n
4 3 54 2 3 2 (5 ) 2 n
nS n
3 2 41 4 2 3 2 (5 ) 22
n
nS n
两式相减得 3 2 5 41 64 (2 2 2 ) (5 ) 22
n n
nS n …………7 分
1
4
18 1 ( )264 ( 5) 211 2
n
nn
1 464 16(2 1) ( 5) 2n nn
5 4 448 2 ( 5) 2 48 ( 3) 2n n nn n
则 5 *96 ( 3)2 ( )n
nS n n N …………………………………………10 分
18. (本小题满分 12 分)在 ABC 中, , ,a b c 分别为角 , ,A B C 的对边,且
(Ⅰ)求角 A ;
(Ⅱ)若 3a ,求 2b c 的最大值.
解:(Ⅰ)由.有,
可得,易得. ……………………………4 分
(Ⅱ)由 2 3sin sin sin
a b c
A B C ,得 2 2 3(sin 2sin )b c B C
2 3 sin 2sin 120 2 3(2sin 3 cos )B B B B ……………………8 分
2 21sin( )B ,其中 3tan , 0 ,2 2
.
由 20 , 3B
,存在 B 使得
2B ,∴sin( )B 的最大值为 1,
∴ 2b c 的最大值为 2 21 . ………………………12 分
19.(本小题满分 12 分)某商场近 5 个月的销售额和利润额如下表所示:
销售额 x /千万元 3 5 6 7 9
利润额 y /百万元 1 3 3 4 5
(Ⅰ)画出散点图,观察散点图,说明两个变量有怎样的相关关系;
(Ⅱ)求出利润额 y 关于销售额 x 的回归直线方程;
6
(Ⅲ)当销售额为 4 千万元时,利用(Ⅱ)的结论估计该商场的利润额(百万元).
1
2
1
n
i i
i
n
i
i
x x y y
b
x x
, a y b x
.
解:(Ⅰ)散点图如图所示:
…………………………………………2 分
两个变量正相关,且具有线性相关关系。 ………………………………………4 分
(Ⅱ)易求得 6, 3.2x y ………………………………………………………………5 分
由公式有 2 2 2 2
3 2.2 1 0.2 0 1 0.8 3 1.8 20 0.653 1 1 3 13b
……………………………7 分
且 3.2 0.65 6 0.7a ……… ……………………………………………………………9 分
则线性回归方程为 0.65 0.7y x ……………………………………………………………10 分
(Ⅲ)当 4x 时,由(Ⅰ)可求得 1.9y ,即利润额约为 1.9 百万元。…………………12 分
20.(本小题满分 12 分)解:(Ⅰ)连接 1BC ,
因为侧面 1 1BB C C 为菱形,
所以 1B C 1BC ,且 1B C 与 1BC 相交于O 点.
因为 AO 平面 1 1BB C C , 1B C 平面 1 1BB C C ,
所以 1B C AO . 又 1BC AO O ,所以 1B C 平面 ABO
因为 AB Ì平面 ABO ,所以 1B C AB …………………………………………4 分
(Ⅱ)由 1AC AB 且 AO 垂直平分 1B C 可知 1ACB 是等腰直角三角形,则 1
1
2AO B C ,
又
得 1 11B C BC B B …………………………………………………………7 分
7
1
2AO ,且等边 1BCB 中, 3
2BO , 故 Rt AOB 中,
221 3 12 2AB
,
又 2
2AC ,易求得等腰 ABC 中 AC 边上的高为 14
4
,
则 1 2 14 7
2 2 4 8ABCS , ………………………………………………………10 分
由
1 1 1
3
8ABC A B C ABCV S h 有 21
7h . …………………………………………12 分
21. (本小题满分 12 分)已知函数 2 lnf x x a x ( )a R .
(Ⅰ)讨论函数 f x 的极值点情况;
(Ⅱ)若 2a ,存在 1x , 2x ,…, 1 ,nx ee
,使得 1 2 1( ) ( ) ( ) ( )n nf x f x f x f x 成立,
求 n 的最大值.
解:(Ⅰ)定义域为 0,
222 a x af x x x x ,………………………………………………………………1 分
故当 0a 时, 0f x ,所以函数 f x 在 0, 上单调递增,无极值点; …………2 分
当 0a 时,令 0f x ,得 2
2
ax ,所以函数 f x 在 2 ,2
a
上单调递增;
令 0f x ,得 2
2
ax ,所以函数 f x 在 20, 2
a
上单调递减,有极小值点
2
2a ,无极大
值点;
综上,当 0a 时,无极值点;
当 0a 时,有极小值点
2
2a ,无极大值点. ……………………………………4 分
(Ⅱ)当 2a 时,由(Ⅰ)知,函数 f x 在 1 ,1e
上单调递减,在 1,e 上单调递增.故
min 1 1f x f , …………………………………5 分
又因为 2
1 1 2 3f e e
, 2 2 25.29 2.7 2 2 2.8 2 5.84f e e ,
故 2
max 2f x f e e . …………………………………7 分
8
故 1 ,x ee
时, 21, 2f x e , …………………………………8 分
由于 2
1 2 12 1 1 1n ne f e f x f x f x f x n f n ,
则 2 1 7n e .
取 1 2 3 4 5 1x x x x x ,
则 2
1 2 5 5 2f x f x f x e ,
故 n 的最大值为 6. …………………………………12 分
22. (本小题满分 12 分)在平面直角坐标系 xOy 中,圆O 为 ABC 的内切圆.其中
( , ), (2, 1), ( 1,3)A m n B C .
(Ⅰ)求圆O 的方程及 A 点坐标;
(Ⅱ)在直线 AO 上是否存在异于 A 的定点Q ,使得对圆 O 上任意一点 P ,都有 PA PQ ( 为
常数 ) ?若存在,求出点Q 的坐标及 的值;若不存在,请说明理由.
解:(Ⅰ)由 (2, 1), ( 1,3)B C 知直线 BC 的方程为 4 3 5 0x y ,
由于圆O 与线段 BC 相切,所以半径 5 15r ,即圆O 的方程为 2 2 1x y .……2 分
由题意 2 2 1x y 与线段 AC 相切,所以线段 AC 方程为 1x .即 1m .
又 2 2 1x y 与线段 AB 也相切,所以线段 AB 方程为 1y .即 1n .
故 1, 1A .…………………………………………………………………………………4 分
(Ⅲ)设 0 0( , ), ( , )Q x y P x y .则 2 2( 1) ( 1)PA x y , 2 2
0 0( ) ( )PQ x x y y .
若在直线 AO 上存在异于 A 的定点Q ,使得对圆O 上任意一点 P ,
都有 PA PQ ( 为常数 ) ,等价于 2 2 2 2
0 0( 1) ( 1) ( ) ( )x y x x y y
对圆O 上任意点 ( , )P x y 恒成立.…………………………………………………………6 分
即 2 2 2 2 2 2
0 0( 1) ( 1) ( ) ( )x y x x y y .
整理得 2 2 2 2 2 2 2 2
0 0 0 0(1 )( ) (2 2 ) (2 2 ) 2 ( ) 0x y x x y y x y .
因为点Q 在直线 AO 上,所以 0 0x y .由于 P 在圆O 上,所以 2 2 1x y .
故 2 2 2 2
0 0(2 2 )( ) 3 2 0x x y x 对任意 [ 2, 2]x y 恒成立. ……8 分
9
所以
2
0
2 2 2
0
2 2 0,
3 2 0.
x
x
显然 0 ,所以 0 2
1x .故 2
2
23 0 ,
因为 0 ,解得 2 或 1 . ……………………………………………………10 分
当 1 时, ( 1, 1)Q ,此时 ,Q A 重合,舍去. ……………………………………11 分
当 2 时, 1 1( , )2 2Q ,
综上,存在满足条件的定点 1 1( , )2 2Q ,此时 2 .………………………………12 分
10