- 484.00 KB
- 2024-01-05 发布
2018届内蒙古阿拉善左旗高级中学
高三第三次模拟考试
数学(文)试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第II卷第(22)~(23)题为选考题,其它题为必考题。考生作答时,将答案答在答题卡上,在本试卷上答题无效。
第Ⅰ卷(选择题)
一、选择题(本大题共12个小题,每小题5分,共60分.)
1.已知集合,,则( )
A. B. C. D.
2.已知(),其中为虚数单位,则( )
A. -3 B.-2 C. -1 D.1
3.设是等差数列的前项和,若,则( )
A.81 B.79 C.77 D.75
4.设满足约束条件,则的最大值是( )
A.-3 B.-6 C.15 D.12
5.已知,则( )
A. B. C. D.
6. 某程序框图如图所示,则该程序运行后输出的值是( )
A.0 B.-1 C.-2 D.-8
7.若双曲线:(,)的左、右焦点分别是,,为双曲线上一点,且,,,则双曲线的离心率为( )
A. B. C. D.
8.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k.据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
9.从集合中随机抽取一个数,从集合中随机抽取一个数,则向量与向量垂直的概率为( )
A. B. C. D.
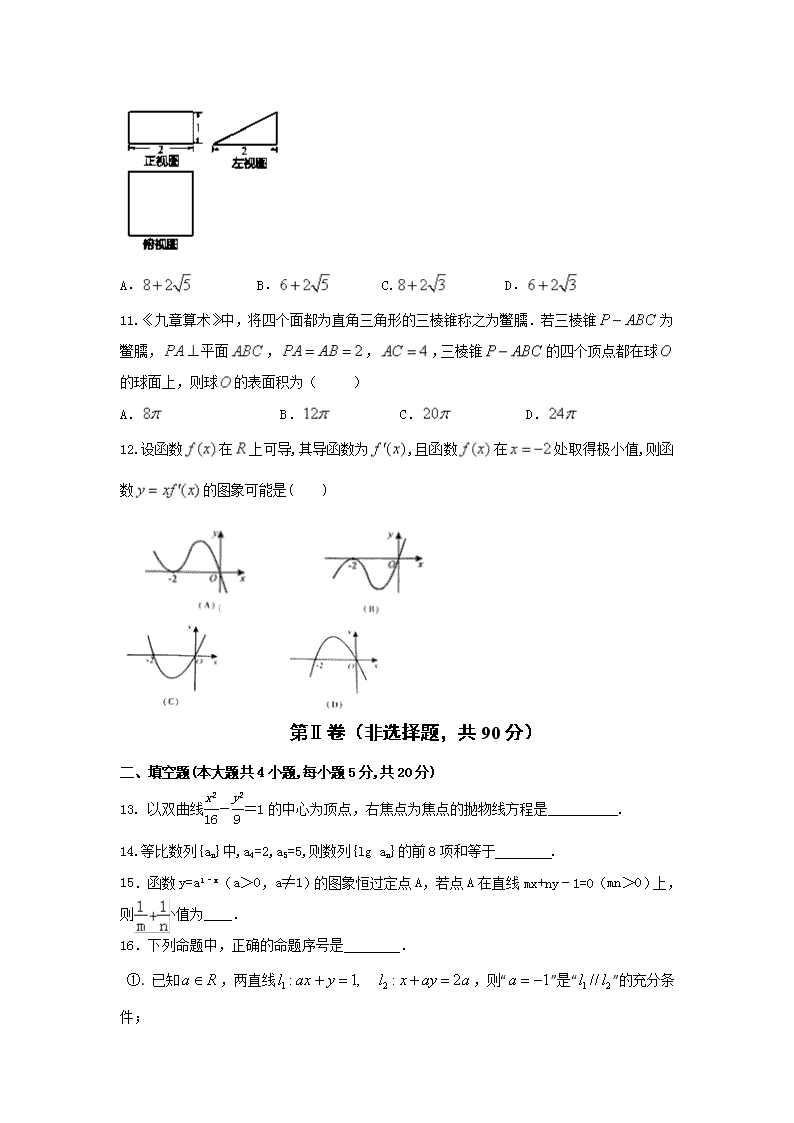
10.某几何体的三视图如图所示,则该几何体的表面积为( )
A. B. C. D.
11.《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥为鳖臑,平面,,,三棱锥的四个顶点都在球的球面上,则球的表面积为( )
A. B. C. D.
12.设函数在上可导,其导函数为,且函数在处取得极小值,则函数的图象可能是( )
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 以双曲线-=1的中心为顶点,右焦点为焦点的抛物线方程是__________.
14.等比数列{an}中,a4=2,a5=5,则数列{lg an}的前8项和等于 .
15.函数y=a1﹣x(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny﹣1=0(mn>0)上,则的最小值为 .
16.下列命题中,正确的命题序号是 .
①. 已知,两直线 ,则“”是“”的充分条件;
②. 命题“,”的否定是“,”;
③.“”是“”的必要条件;
④. 已知,则“”的充要条件是“” .
三、解答题(解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知内接于单位圆,角且的对边分别为,且.
1.求的值; 2.若 求的面积.
18.(本小题满分12分)如图,菱形ABCD的边长为12,∠BAD=60°,AC交BD于点O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M,N分别是棱BC,AD的中点,且DM=6.
(Ⅰ)求证:OD ⊥平面ABC; (Ⅱ)求三棱锥M -ABN的体积.
19.(本小题满分12分)阿拉善盟某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示.
下面是年龄的分布表:
区间
[25,30)
[30,35)
[35,40)
[40,45)
[45,50)
人数
28
a
b
(Ⅰ)求正整数的值;
(Ⅱ)现要从年龄低于40岁的员工用分层抽样的方法抽取42人,则年龄在第组得员工人数分别是多少?
(Ⅲ)为了估计该单位员工的阅读倾向,现对该单位所有员工中按性别比例抽查的40人是否喜欢阅读国学类书籍进行了调查,调查结果如下所示:(单位:人)
喜欢阅读国学类
不喜欢阅读国学类
合计
男
14
4
18
女
8
14
22
合计
22
18
40
根据表中数据,我们能否有的把握认为该位员工是否喜欢阅读国学类书籍和性别有关系?
喜欢阅读国学类
不喜欢阅读国学类
合计
男
14
4
18
女
8
14
22
合计
22
18
40
附:,其中.
0.05
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
20.(本小题满分12分)已知函数在 处取得极值.
(1)确定的值;
(2)若,讨论的单调性.
21.(本小题满分12分)已知离心率为的椭圆过点,点分别为椭圆的左、右焦点,过的直线与交于两点,且
.
(1)求椭圆的方程;
(2)求证:以为直径的圆过坐标原点.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.在直角坐标系中,直线的方程为, 曲线的参数方程为
(1).已知在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点, 以轴正半轴为极轴)中,求直线的极坐标方程;
(2).设点是曲线上的一个动点,求它到直线的距离的最小值
23.已知函数
(1).当时,求关于的不等式的解集
(2).若关于的不等式有解,求的取值范
阿左旗高级中学2018届高三年级第三次模拟考试
第Ⅰ卷(选择题)
一、选择题(本大题共12个小题,每小题5分,共60分.)
CAADC BACBA CC
第Ⅱ卷(非选择题,共90分)
本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.
二、填空题(本大题共4小题,每小题5分,共20分)
13. 以双曲线-=1的中心为顶点,右焦点为焦点的抛物线方程是__________.[答案] y2=20x
14.等比数列{an}中,a4=2,a5=5,则数列{lg an}的前8项和等于 .
解析:因为等比数列{an}中a4=2,a5=5,所以a4·a5=2×5=10,所以数列{lg an}的前8项和
S=lg a1+lg a2+…+lg a8=lg(a1·a2…a8)=lg(a4·a5)4=4lg(a4·a5)=4lg 10=4.答案:4
15.函数y=a1﹣x(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny﹣1=0(mn>0)上,则的最小值为 .
解:由已知定点A坐标为(1,1),由点A在直线mx+ny﹣1=0上,∴m+n=1,
又mn>0,∴m>0,n>0,∴=()(m+n)==2++≥2+2•=4,
当且仅当两数相等时取等号.故答案为4..
16.下列命题中,正确的命题序号是 .答案 ①③④
①. 已知,两直线 ,则“”是“”的充分条件;
②. 命题“,”的否定是“,”;
③.“”是“”的必要条件;
④. 已知,则“”的充要条件是“” .
三、解答题(解答应写出文字说明、证明过程或演算步骤)
18.(本小题满分12分)
已知内接于单位圆,角且的对边分别为,且.
1.求的值; 2.若求的面积.
答案: 1.∵
又
所以,即
2.由(1)知,
由,
得 因此
18.(本小题满分12分)
【解析】:(Ⅰ)证明:是菱形,∴,
在中,, ∴
又是中点, ∴
, ∴
面,∴面. ………………6分
(Ⅱ)解:取线段AO的中点E,连接NE.∵N是棱AD的中点,∴.
∵由(Ⅰ)得面,∴面,在中,
∴. ……………12分
19.(本小题满分12分)
喜欢阅读国学类
不喜欢阅读国学类
合计
男
14
4
18
女
8
14
22
合计
22
18
40
【解析】:(Ⅰ)总人数:,
第3组的频率是:
所以 …………………………………………………4分
(Ⅱ)因为年龄低于40岁的员工在第1,2,3组,共有(人),
利用分层抽样在168人中抽取42人,每组抽取的人数分别为:
第1组抽取的人数为(人),第2组抽取的人数为(人),
第3组抽取的人数为(人),所以第1,2,3组分别抽7人、7人、28人.…8分
(Ⅲ)假设:“是否喜欢看国学类书籍和性别无关系”,根据表中数据,
求得的观测值,
查表得,从而能有的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系…………………………12分
20.(本小题满分12分)
答案: 1.对求导得.因为在处取得极值,所以,即,解得.
2.由1得,
故
令,解得或或.当时,,故为减函数;
当时,,故为增函数;当时,,故为减函数;当时,,故为增函数;
综上可知在和上为减函数,在和上为增函数.
21.(本小题满分12分)
已知离心率为的椭圆过点,点分别为椭圆的左、右焦点,过的直线与交于两点,且.
(1)求椭圆的方程;
(2)求证:以为直径的圆过坐标原点.
解析
(Ⅱ)由(1)知, ;令, ;当直线的斜率不存在时,直线方程为;此时, ,不满足;设直线方程为;
代入椭圆方程得:
韦达定理: , ;所以, ,
;所以, ;
点到直线的距离为;所以,由得: ;
所以,以为直径的圆过坐标原点
选考部分
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22、在直角坐标系中,直线的方程为, 曲线的参数方程为
1.已知在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点, 以轴正半轴为极轴)中,求直线的极坐标方程;
2.设点是曲线上的一个动点,求它到直线的距离的最小值
答案: 1. 2.
23、已知函数
1.当时,求关于的不等式的解集
2.若关于的不等式有解,求的取值范围
答案: 1.解:当时,不等式为,
若,则即 若,则,舍去
若,则,即,综上,不等式的解集为
2.因为得到的最小值为
所以,所以