- 619.00 KB
- 2023-12-31 发布
雨花台区2011-2012学年度中考模拟试卷(一)
数 学
2012.04
注意事项:
1. 本试卷共6页.全卷满分120分.考试时间120分钟.考生答题全部答在答卷纸上,答在试卷上无效.
2. 将自己的姓名、准考证号用黑色字迹的0.5毫米签字笔填写在答卷纸的指定位置上.
3. 答案必须使用0.5毫米黑色签字笔书写,字迹工整、笔迹清楚;作图必须使用2B铅笔作答,并请加黑加粗,描写清楚.
4. 请按题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.
一、选择题(本大题共6小题,每小题2分,共计12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答卷纸相应位置上)
1.-2的倒数是 ( ▲ )
A. B. C. D.
2.下列运算正确的是 ( ▲ )
A. B. C. D.
3.在等边三角形、平行四边形、正方形、圆、正七边形这五个图形中,既是中心对称图形又是轴对称图形的个数是 ( ▲ )
A.1个 B.2个 C.3个 D.4个
4.下列几何体中,主视图与左视图完全相同的是 ( ▲ )
A.长方体 B.三棱锥 C. 三棱柱 D.圆柱
5.2012年2月29日,国务院批准发布的《环境空气质量标准》中,增加了细颗粒物(PM2.5)年均、日均浓度限值。2012年3月30日江苏省环境监测中心公布了全省17个PM2.5监测点的日均值如下(单位:微克/立方米):94,141,118,60,88,84,66,66,73,78,89,149,130,131,113,97,180。该组数据的极差和中位数分别是 ( ▲ )
A.86,94 B.86,73 C.120,94 D.120,73
6.我市为迎接2014青奥会的召开,现对某景观道路进行拓宽改造。工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了拓宽改造任务。下面能反映该工程尚未改造的道路y(米)与时间x(天)的函数关系的大致图像是 ( ▲ )
A. B. C. D.
二、填空题(本大题共有10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答卷纸相应位置上)
7.函数中自变量 x 的取值范围是 ▲ .
8.因式分解: ▲ .
9.雨花台风景区为国家首批4A级旅游区,面积约为1540000平方米,绿地覆盖率达90%以上,数据“1540000”用科学记数法表示为 ▲ .
10.反比例函数的图象在每一象限内随的增大而增大,则的取值范围是 ▲ .
11.已知函数与的交点坐标为(-1,1),则方程组 的解为 ▲ .
12.如图是一环形靶,AB、CD是靶上两条互相垂直的直径,一人随意向靶射击,中靶后,子弹击中靶上阴影区域的概率为 ▲ .
13.如图,内接于⊙O,,cm,则劣弧AB的长为 ▲ cm(结果保留).
(第14题)
(第12题)
(第13题)
14.如图,已知点G是梯形的中位线上任意一点,若梯形的面积为20cm2,则图中阴影部分的面积为 ▲
15.若关于的方程有实数根,则的值可以是 ▲ .(任意给出一个符合条件的值即可)
16.已知等腰的两条边长分别为、,是底边上的高,⊙的半径为,⊙与⊙相切,那么⊙的半径是 ▲ .
三、解答题(本大题共12小题,共计88分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17.(本题满分6分)求不等式组的整数解.
18.(本题满分6分)计算:°.
19.(本题满分6分)先化简,然后从的范围内选取一个合适的整数作为 的值代入,求原式的值.
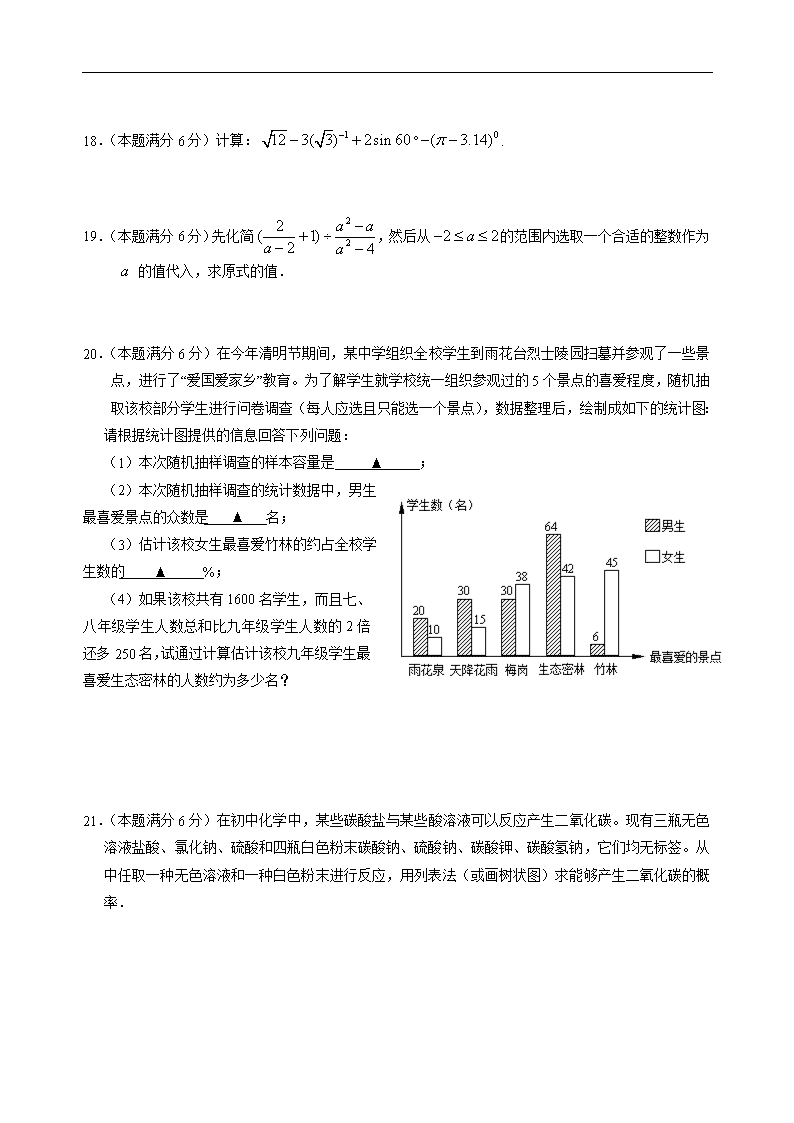
20.(本题满分6分)在今年清明节期间,某中学组织全校学生到雨花台烈士陵园扫墓并参观了一些景点,进行了“爱国爱家乡”教育。为了解学生就学校统一组织参观过的5个景点的喜爱程度,随机抽取该校部分学生进行问卷调查(每人应选且只能选一个景点),数据整理后,绘制成如下的统计图:
请根据统计图提供的信息回答下列问题:
(1)本次随机抽样调查的样本容量是 ▲ ;
(2)本次随机抽样调查的统计数据中,男生最喜爱景点的众数是 ▲ 名;
(3)估计该校女生最喜爱竹林的约占全校学生数的 ▲ %;
(4)如果该校共有1600名学生,而且七、八年级学生人数总和比九年级学生人数的2倍还多250名,试通过计算估计该校九年级学生最喜爱生态密林的人数约为多少名?
21.(本题满分6分)在初中化学中,某些碳酸盐与某些酸溶液可以反应产生二氧化碳。现有三瓶无色溶液盐酸、氯化钠、硫酸和四瓶白色粉末碳酸钠、硫酸钠、碳酸钾、碳酸氢钠,它们均无标签。从中任取一种无色溶液和一种白色粉末进行反应,用列表法(或画树状图)求能够产生二氧化碳的概率.
22.(本题满分6分)阅读下列材料并解答相关问题:
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.
数学老师给小明同学出了一道题目:在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使,;
小明同学的做法是:由勾股定理,得,,于是画出线段AB、AC、BC,从而画出格点△ABC.(1)请你参考小明同学的做法,在图2正方形网格(每个小正方形边长 为1)中画出格点△(点位置如图所示),使==5,.(直接画出图形,不写过程);
(2)观察△ABC与△的形状,猜想∠BAC与∠有怎样的数量关系,并证明你的猜想.
23.(本题满分7分)如图是大型输气管的截面图(圆形),小丽为了计算大型输气管的直径,在圆形弧上取了,两点并连接,在劣弧AB上取中点连接,经测量米,°,根据这些数据请你帮小丽计算出大型输气管的直径(精确到米).
(°,°,°)
x(小时)
y(千米)
450
10
4 5
O
F
C E
D
24.(本题满分7分)A、B两城间的公路长为450千米,甲、乙两车同时从A城出发沿这一公路驶向B城,甲车到达B城1小时后沿原路返回.如图是它们离A城的路程y(千米)与行驶时间 x(小时)之间的函数图像.
(1)求甲车返回过程中y与x之间的函数关系式,并写出变量 的取值范围;
(2)乙车行驶6小时与返回的甲车相遇,求乙车的行驶速度.
25.(本题满分7分)如图,矩形纸片ABCD的边长AB=4,AD=2.翻折矩形纸片,使点A与点C重合,折痕分别交AB、CD于点E、F,
(1)在图中,用尺规作折痕EF所在的直线(保留作图痕迹,不写作法);
(2)求线段EF的长.
A
B
M
N
D
C
26.(本题满分9分)已知:如图,在△ABC中,M是边AB的中点,D是边BC延长线上一点,,DN∥CM,交边AC于点N.
(1)求证:MN∥BC;
(2)当∠ACB为何值时,四边形BDNM是等腰梯形?并证明你的猜想.
27.(本题满分10分)已知抛物线过点,,三点.
(1)求该抛物线的函数关系式;
(2)若抛物线的顶点为P,连接PA、AC、CP,求△PAC的面积;
(3)过点C作轴的垂线,交抛物线于点D,连接PD、BD,BD交AC于点E,判断四边形PCED的形状,并说明理由.
28.(本题满分12分)如图,在Rt△ABC中,∠C=90°,AC=4㎝,BC=5㎝,D是BC边上一点,CD=3㎝,点P为边AC上一动点(点P与A、C不重合),过点P作PE// BC,交AD于点E.点P以1㎝/s的速度从A到C匀速运动。
(1)设点P的运动时间为,DE的长为(㎝),求关于的函数关系式,并写出的取值范围;
(2)当为何值时,以PE为半径的⊙E与以DB为半径的⊙D外切?并求此时∠DPE的正切值;
(3)将△ABD沿直线AD翻折,得到△AB’D,连接B’C.如果∠ACE=∠BCB’,求的值.
雨花台区2011-2012学年度中考模拟试卷(一)
数学参考答案
一、选择题
1.C 2.B 3.B 4.D 5.C 6.D
二、填空题
7. 8. 9. 10. 11. 12. 13. 14. 5 15. 答案不唯一(即可,如等) 16. 或
三、解答题:
17.解:
解不等式① 得,; ………………………………………………………2分
解不等式② 得,. ………………………………………………………4分
所以不等式组的解集是 ……… ……………………………………5分
不等式组的整数解是 …………………………………………………6分
18.解:原式………………………………………………4分
………………………………………………5分
………………………………………………6分
19.解:原式…………………………………2分
…………………………………3分
…………………………………4分
∵且,,
∴只能取 ……… ……………………………………5分
当时,原式……… ……………………………………6分
20.解:(1) 300 ……… ……………………………………1分
(2) 30 ……… ……………………………………2分
(3) 15 ……… ……………………………………3分
(4)设九年级学生数为名,根据题意得:
解得:……… ……………………………………5分
(名)
答:九年级学生最喜爱生态密林的人数约为159名……… ……………6分
21.解:用A、B、C分别表示盐酸、氯化钠、硫酸,用1、2、3、4分别表示碳酸钠、硫酸钠、碳酸钾、碳酸氢钠。
列表法
A
B
C
1
A1
B1
C1
2
A2
B2
C2
3
A3
B3
C3
4
A4
B4
C4
或画树状图
从表(或树状图)中可以看出,共有12种等可能的结果,其中能产生二氧化碳的结果有6种,所以
本题满分6分,其中列表或画树状图正确4分,结果正确2分。
22.解:(1)如右图,画图正确……………………………2分
(2)∠BAC﹦∠B’A’C’ …………………3分
证明:∵,,
∴
∴△ABC∽△A’B’ C’ ……………………………5分
∴∠BAC﹦∠B’A’C’ ……………………………6分
23.解:设圆心为,连接、交于…1分
∵是弧的中点,是半径
∴, ……………………2分
在中 米,
∴ ………3分
……………………………4分
在中,设圆的半径为
……………………………5分
(米) ……………………………6分
答:大型输气管的直径约为米 ……………………………7分
(其它解法,正确合理可参照给分。)
24.解:(1)设甲车返回过程中y与x之间的函数解析式为,……………1分
∵图像过(5,450),(10,0)两点, …………………………………………2分
∴ ………………………………………………………………3分
解得 ∴.……………………………………………4分
的取值范围为5≤≤10.…………………………………………………………5分
(2)当时,,……………………………………………6分
(千米/小时). ………………………………………………………7分
25.解:(1) 作图正确…………………………………………………………………2分
(2)∵矩形ABCD,
∴,.
∵在Rt△ABC中,AB=4,AD=2
∴由勾股定理得:.……………3分
设与相交与点,
由翻折可得 . ……………………………………………4分
.
∵在Rt△ABC中, ,
在Rt△AOE中,.
∴, ……………………………5分
∴. ……………………………6分
同理:.
∴. ……………………………………………………………7分
(其它解法,正确合理可参照给分。)
26.解:(1)证法一:取边BC的中点E,连接ME.……1分
∵BM=AM,BE=EC,∴ME∥AC.…………2分
∴∠MEC=∠NCD.
∵,∴.
∵DN∥CM,∴∠MCE=∠D.
∴△MEC≌△NCD.………………………………………………………3分
∴.
又∵CM∥DN,∴四边形MCDN是平行四边形.………………………4分
∴MN∥BC.…………………………………………………………………5分
证法二:延长CD到F,使得,连接AF.…………1分
∵,,
∴.……………2分
∵,∴MC∥AF.
∵MC∥DN,∴ND∥AF.………3分
又∵,∴.……4分
∴MN∥BC.…………………………5分
(2)解:当∠ACB=90°时,四边形BDNM是等腰梯形.…………………………6分
证明如下:
∵MN∥BD,BM与DN不平行,∴四边形BDNM是梯形.……………7分
∵∠ACB=90°,,∴. …………………8分
∵,∴BMDN.
∴四边形BDNM是等腰梯形.………………………………………………9分
(其它解法,正确合理可参照给分。)
27.(1)由题意得: 解得: …………2分
∴ …………………………………………3分
(2) ∴ ……………………4分
∴,,
∵
∴ ……………………………………………………5分
∴ …………………………………6分
(3)四边形PCED是正方形
∵点C与点D关于抛物线的对称轴对称,点P为抛物线的顶点
∴点D的坐标为,=…………………………………7分
∴直线的函数关系式是:
直线的函数关系式是:
∴∥
同理可得:∥
∴四边形PCED是菱形 …………………………………9分
又∵
∴四边形PCED是正方形 …………………………………10分
(其它解法,正确合理可参照给分。)
28.解:(1)∵在Rt△ABC中,AC=4,CD=3,∴AD=5,……………………1分
∵PE// BC,,∴,∴,…………………………2分
∴,∴,………………………………………………3分
即,()…………………………………………………4分
(2)当以PE为半径的⊙E与DB为半径的⊙D外切时,有
DE=PE+BD,即,…………………………………………5分
解之得,∴, …………………………………………………6分
∵PE// BC,∴∠DPE=∠PDC, ………………………………………………7分
在Rt△PCD中,
tan=;∴tan=………………………………8分
(3) 延长AD交BB/于F,则AF⊥BB/,
∴,又,
∴
∴∽,………………………9分
∴BF=,所以BB/= ,……………………10分
∵∠ACE=∠BCB/,∠CAE=∠CBB/,
∴∽,∴,………………11分
∴ …………………………………………………………………12分
(其它解法,正确合理可参照给分。)