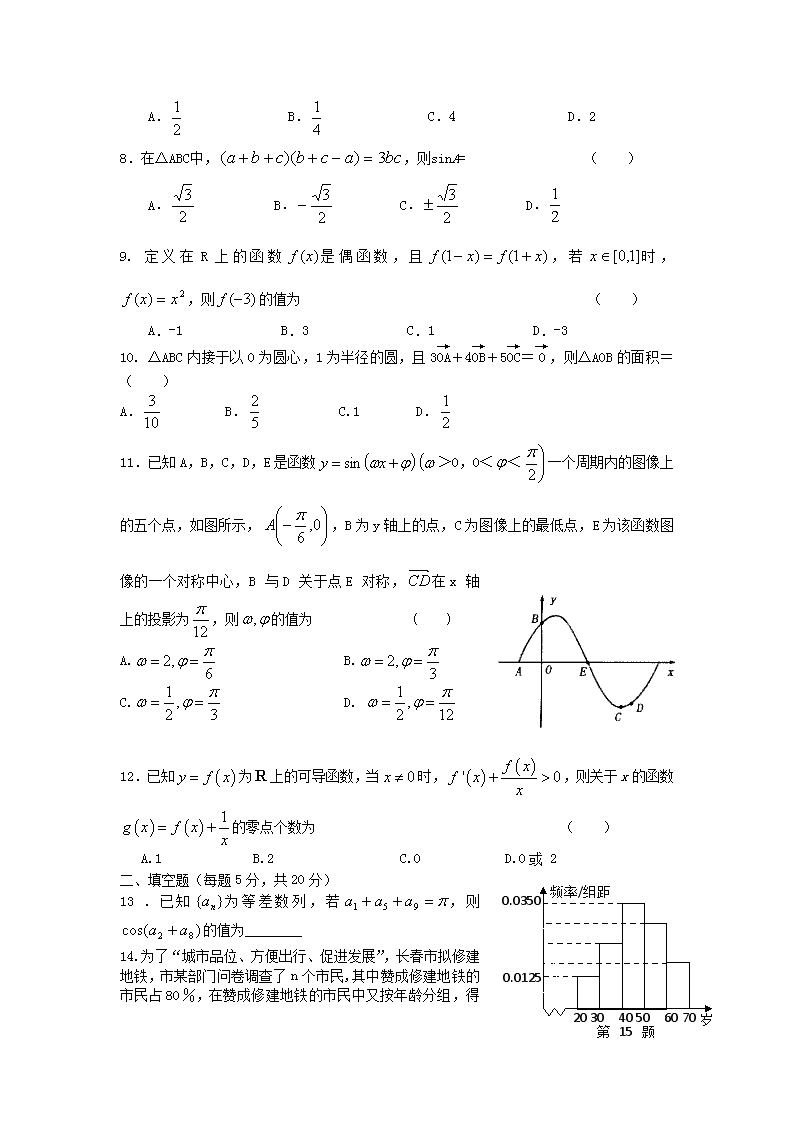- 512.50 KB
- 2023-12-30 发布
吉林省实验中学2012—2013学年度下学期期末考试
高二数学理试题
一、选择题(每题5分,共60分)
1.若集合,集合= ( )
A. B.
C. D.
2.下列各函数中值域为的是 ( )
A. B. C. D.
3.若一个正三棱柱的三视图如图所示,则这个正三棱柱的高和底面边长分别为( )
2
2
正视图
侧视图
俯视图
A.2,2
B.2,2
C.4,2
D.2,4
4.已知实数,则“”是 “”的 ( )
A.充分不必要条件B.必要不充分条件 C.充要条件D.既不充分也不必要条件
否
开始
结束
输出
是
输入
5.运行右图所示的程序框图.若输入,则输出的值为 ( )
A. B.
C. D.
6.已知长方体的全面积为11,其12条棱的长度之和为
24,则这个长方体的一条对角线长为 ( )
A. B. C.5 D.6
7.若直线经过圆的圆心,则的最小值是 ( )
A. B. C.4 D.2
8.在△ABC中,,则sinA= ( )
A. B. C. D.
9. 定义在R上的函数是偶函数,且,若时,,则的值为 ( )
A.-1 B.3 C.1 D.-3
10. △ABC内接于以O为圆心,1为半径的圆,且3+4+5=,则△AOB的面积= ( )
A. B. C.1 D.
11.已知A,B,C,D,E是函数>0,0<<一个周期内的图像上的五个点,如图所示,,B为y轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称,在x轴上的投影为,则的值为 ( )
A. B.
C. D.
12.已知为上的可导函数,当时,,则关于x的函数的零点个数为 ( )
A.1 B.2 C.0 D.0或 2
20 30 40 50 60 70
岁
频率/组距
第15题图
0.0350
0.0125
二、填空题(每题5分,共20分)
13.已知为等差数列,若,则的值为
14.为了“城市品位、方便出行、促进发展”,长春市拟修建地铁,市某部门问卷调查了n个市民,其中赞成修建地铁的市民占80%,在
赞成修建地铁的市民中又按年龄分组,得样本频率分布直方图如图,其中年龄在岁的有400人,岁的有m人,则n= , m=
15.已知,,,和的夹角是锐角,则实数的取值范围是 .
16.已知函数,若时,不等式 恒成立,则实数t的取值范围是 .
三解答题
17.(12分)已知关于的一元二次方程.
(Ⅰ)若是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(Ⅱ)若,求方程没有实根的概率.
18. (满分12分)已知圆C:。(1)若圆C的切线在x轴、y轴上的截距相等,求切线方程;(2)从圆C外一点P()向该圆引一条切线,切点为M且有(O为原点),求使取得最小值时点P的坐标。
19.(满分12分)如图,在四棱锥S-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.
(1)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(2)求证:平面BDE⊥平面SAC;
(3)当二面角E-BD-C的大小为45°时,试判断点E在SC上的位置,并说明理由.
20.(满分12分)数列:满足
(Ⅰ) 设,求证是等比数列;(Ⅱ) 求数列的通项公式;
(Ⅲ)设,数列的前项和为,求证:
21.已知函数
(1)求的单调区间;
(2)求证:
选考题(本小题满分10分)(请考生在22,23,24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡把所选题目的题号涂黑)
22.(本小题满分10分)选修4—1:几何证明选讲
如图,内接于⊙O,且AB=AC,过点A的直线交⊙O于点P,交BC的延长线于点D。 (I)求证:
(II)若,⊙O的半径为1,且P为弧的中点,求AD的长。
23.本题满分10分)选修4—4:坐标与参数方程
已知直线的极坐标方程为,圆的参数方程为(其中为参数)
(1)将直线的极坐标方程化为直角坐标方程;(2)求圆上的点到直线的距离的最小值
24.选修4—5:不等式选讲
已知函数
(1)当a=0时,解不等式
(2)若存在成立,求实数a的取值范围。
参考答案
一.选择题(本大题共12小题,每小题5分,共计60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
D
B
B
C
C
A
C
D
B
C
二.填空题(本大题共20小题,每小题5分,共计20分)
13. 14. n= 4000 , m= 1120
15. 且 16. _____.
三、解答题
17.(满分12分)
解:(Ⅰ)基本事件共有36个,方程有实根,
方程有根等价于Δ≥0, (a-2)2+b2≥16.
设“方程有两个实根”为事件,则事件包含的基本事件共36-14=22个,
故所求的概率为; ……………6分
(Ⅱ)试验的全部结果构成区域,其面积为
设“方程无实根”为事件,则构成事件的区域为
,
其面积为
故所求的概率为 ………………12分
18. (满分12分)
解: ( 1)将圆C配方得(x+1)2+(y-2)2=2.
①当直线在两坐标轴上的截距为零时,设直线方程为y=kx,由直线与圆相切得
=,即k=2±,从而切线方程为y=(2±)x . .……………………3分
②当直线在两坐标轴上的截距不为零时,设直线方程为x+y-a=0,
由直线与圆相切得x+y+1=0,或x+y-3=0.∴所求切线的方程为y=(2±)x
x+y+1=0或x+y-3=0 .……………………6分
(2)由|PO|=|PM|得,x12+y12=(x1+1)2+(y1-2)2-2⇒2x1-4y1+3=0. .…………8分
即点P在直线l:2x-4y+3=0上,|PM|取最小值时即
|OP|取得最小值,直线OP⊥l,∴直线OP的方程为2x+y=0. .……………………10分
解方程组得P点坐标为 ..……………………12分
19. (满分12分)
证明:(Ⅰ)连接,由条件可得∥.
因为平面,平面,
所以∥平面.
(Ⅱ)法一:证明:由已知可得,,是中点,
所以,
又因为四边形是正方形,所以.
因为,所以.
又因为,所以平面平面. -
(Ⅱ)法二:证明:由(Ⅰ)知,.
建立如图所示的空间直角坐标系.
设四棱锥的底面边长为2,
则,,,
,,.
所以,.
设(),由已知可求得.
所以,.
设平面法向量为,
则 即
令,得.
易知是平面的法向量.
因为,
所以,所以平面平面. -------------------8分
(Ⅲ)解:设(),由(Ⅱ)可知,
平面法向量为.
因为,
所以是平面的一个法向量.
由已知二面角的大小为.
所以,
所以,解得.
所以点是的中点. ----------------12分
20.(满分12分)
解:(Ⅰ)由得 ……………………2分
,即 , ……………………4分
是以2为公比的等比数列 ……………………5分
(Ⅱ) 又
即 , ……………………6分
故 ……………………7分
(Ⅲ) ……………………9分
……………………10分
又 ……………………12分
21.(满分12分).
解:(1), ………………1分
…………3分
令上单调递减;
令上单调递增。
故增区间为减区间为(-1,0) ……………………5分
(2) ……………………6分
令
…………7分
令则
令
当在(-1,0)上单调递增;
当上单调递减,
故上单调递减; …………9分
当时,,即,则在(-1,0)上单调递增;当即上单调递减…………11分
故 …………12分
22.(本小题满分10分)选修4—1:几何证明选讲
23.本题满分10分)选修4—4:坐标与参数方程
解:(1)极点为直角坐标原点O,,
∴,可化为直角坐标方程:x+y-1=0. ……………………5分
(2)将圆的参数方程化为普通方程:,圆心为C(0,-2),
∴点C到直线的距离为,
∴圆上的点到直线距离的最小值为。 ……………………5分
24. 本题满分10分)
解:(1)由|x+1|≥2|x|,得x2+2x+1≥4x2,解得-≤x≤1.
所以不等式的解集是[-,1]. ……………………10分
(2)由题意可知,存在x∈R,使得|x+1|-2|x|≥a.
令φ(x)=
当x<-1时,φ(x)<-2;当-1≤x<0时,-2≤φ(x)<1;当x≥0时,φ(x)≤1.
综上可得:φ(x)≤1,即a≤1. ……………………10分