- 1.63 MB
- 2023-12-30 发布
福建省闽侯第四中学2018届高三上学期期中
数学(文)试题
一、选择题:本大题共 12 小题,每小题5分,共60分.在每小题给出的四个选项中有且只有一项是符合题目要求的,把答案填在答题卡的相应位置.)
1.设集合,,则中元素的个数是( )
A. B. C. D.
2.复数满足,则( )
A. B. C. D.
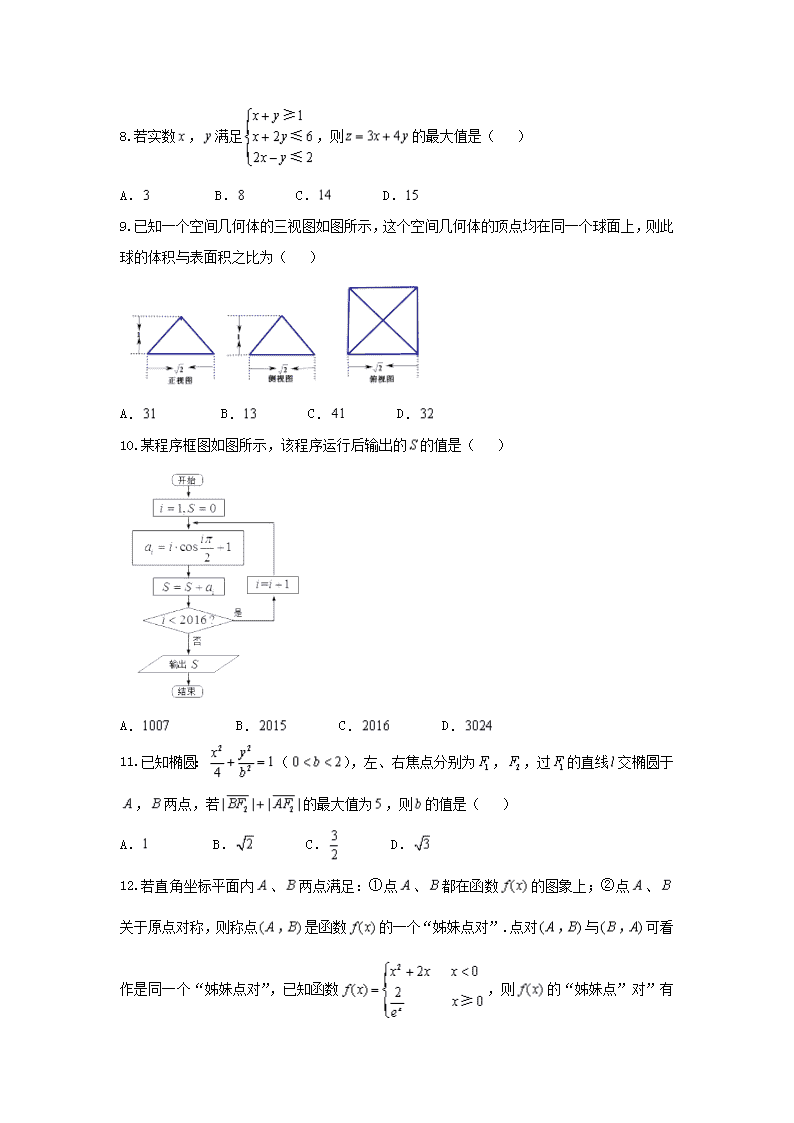
3.有个不同的社团,甲、乙两名同学各自参加其中个社团,每位同学参加各个社团的可能性相同,则这两位同学参加同一个社团的概率为( )
A. B. C. D.
4.下列判断错误的是( )
A.若为假命题,则,至少之一为假命题
B.命题“,”的否定是“,”
C.“若且,则”是真命题
D.“若,则”的否命题是假命题
5.已知双曲线:(,)的右焦点与抛物线的焦点重合,且其渐近线方程为,则双曲线的方程为( )
A. B. C. D.
6.将函数的图象上各点的横坐标压缩为原来的倍(纵坐标不变),所得函数在下面哪个区间单调递增( )
A. B. C. D.
7.已知是公差不为的等差数列的前项和,且,,,成等比数列,则等于( )
A. B. C. D.
8.若实数,满足,则的最大值是( )
A. B. C. D.
9.已知一个空间几何体的三视图如图所示,这个空间几何体的顶点均在同一个球面上,则此球的体积与表面积之比为( )
A. B. C. D.
10.某程序框图如图所示,该程序运行后输出的的值是( )
A. B. C. D.
11.已知椭圆:(),左、右焦点分别为,,过的直线交椭圆于,两点,若的最大值为,则的值是( )
A. B. C. D.
12.若直角坐标平面内、两点满足:①点、都在函数的图象上;②点、关于原点对称,则称点是函数的一个“姊妹点对”.点对与可看作是同一个“姊妹点对”,已知函数,则的“姊妹点”对”有
( )
A.个 B.个 C.个 D.个
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.
13.已知数列满足:,,,则 ..
14.在中,,且,,则 ..
15.已知,,且,则的最小值为 ..
16.函数,若方程恰有四个不等的实数根,则实数的取值范围是 .
三、解答题(本大题共 6 小题,共 70 分.解答应写出必要的文字说明、证明过程或演算步骤.)
17.已知向量,(),若,且的图象上两相邻对称轴间的距离为.
(Ⅰ)求的单调递减区间;
(Ⅱ)设的内角,,的对边分别为,,,且满足,,,求,的值.
18.为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了人,他们年龄大点频数分布及支持“生育二胎”人数如下表:
年龄
频数
支持“生育二胎”
(Ⅰ)由以上统计数据填下面乘
年龄不低于岁的人数
年龄低于岁的人数
合计
列联表,并问是否有的把握认为以岁为分界点对“生育二胎放开”政策的支持度有差异:
支持
不支持
合计
(Ⅱ)若对年龄在的的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据:,.
19.已知直角梯形中,,,,,,为的中点,过作 ,将四边形沿折起使面面.
(1)若为的中点,求证:面;
(2)若,试求多面体体积.
20.定义:在平面内,点到曲线上的点的距离的最小值称为点到曲线的距离.在平面直角坐标系中,已知圆:及点,动点到圆的距离与到点的距离相等,记点的轨迹为曲线为.
(Ⅰ)求曲线
的方程;
(Ⅱ)过原点的直线(不与坐标轴重合)与曲线交于不同的两点,,点在曲线上,且,直线与轴交于点,设直线,的斜率分别为,,求.
21.已知函数,()
(Ⅰ)求函数的单调区间;
(Ⅱ)证明:当时,对于任意,,总有成立,其中是自然对数的底数.
请考生在第22、23、24 三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡上把所选题目对应题号上方的方框涂黑.
22.选修 4-1:几何证明选讲
已知点在圆直径的延长线上,切圆于点,分别交,于点,,.
(1)求证:为的平分线;
(2)若,求的值.
23.选修 4-4:坐标系与参数方程在直角坐标系中,以坐标原点为极点,轴正半轴为极轴建立极坐标系,已知圆的极坐标方程为,从极点作圆的弦,记各条弦中点的轨迹为曲线.
(1)求的极坐标方程;
(2)已知曲线的参数方程为(,为参数,且),与交于点,与交于点,且,求的值.
24.选修 4-5:不等式选讲
已知,,均为正实数,且.
(1)证明:;
(2)求证:.
高三数学(文)答案
一、选择题
1-5:ABACA 6-10:ACCBD 11、12:DC
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(Ⅰ)∵,,
∴
.
∵的图像上两相邻对称轴间的距离为,∴,即.
∴
则.
由,得,,
∴的单调减区间为,
(Ⅱ)由,得,
∵,∴,则,.
由余弦定理得:,即,①
又,②
联立①②解得:,.
18.(Ⅰ)
年龄不低于岁的人数
年龄低于岁的人数
合计
支持
不支持
合计
所以没有的把握认为以岁为分界点对“生育二胎放开”政策的支持度有差异.
(Ⅱ)年龄在中支持“生育二胎”的人分别为,,,,不支持“生育二胎”的人记为,厄从年龄在的被调查人中随机选取两人所有可能的结果有:,,,,,,,,.
设“恰好这两人都支持“生育二胎””为事件,
则事件所有可能的结果有,,,,.
∴
所以对年龄在的被调查人中随机选取两人进行调查时,恰好这两人都支持“生育二胎”的概率为
19.证明:(1)取的中点,连接,,因为,,,且,所以,且,所以四边形为平行四边形,,面,故 面.
解:(2)因为面面,所以,,两两垂直,连接,所求的几何体分为两部分,四棱锥与三棱锥,
,
,
20.解:(Ⅰ)由点到曲线的距离的定义可知,到圆的距离,所以,所以有,由椭圆定义可得点的轨迹为以、
为焦点的椭圆,从而可求出椭圆的方程;(Ⅱ)设,,则,则直线的斜率为,由可得直线的斜率是,记,设直线的方程为,与椭圆方程联立,得到关于的一元二次方程,利用韦达定理用,表示与即可得到结论.
解(Ⅰ)由分析知:点在圆内且不为圆心,故,
所以点的轨迹为以、为焦点的椭圆,
设椭圆方程为(),则,
所以,故曲线的方程为.
(Ⅱ)设(),,则,则直线的斜率为,又,所以直线的斜率是,记,设置的方程为,由题意知,,由得.∴,
∴,由题意知,,
所以,
∴直线的方程为,令,得,即.
可得.
所以,即.
21.解析:(Ⅰ)函数的定义域为,
当时,当变化时,,的变化情况如下表:
当时,当变化时,,的变化情况如下表:
综上所述,
当时,的单调递增区间为,单调递减区间为,;
当时,的单调递增区间为,,单调递减区间为;
(Ⅱ)由(Ⅰ)可知,当时,在区间上单调递增,;
在区间上单调递减,且,所以当时,.
因为,所以,令,得.
①当时,在区间上恒成立
所以函数在区间上单调递增,所以.
所以对于任意,,仍有.
②当时,由,得;由,得,所以函数在区间上单调递增,在区间上单调递减,所以.
因为
所以对任意,,总有.
22.(Ⅰ)证明:∵为圆的切线,∴,
又∵为直径,,∴.
又∵,,
∴,
∴为的平分线
(Ⅱ)解:,∴,
又,
∴,
∴
23.解:(Ⅰ)设上任意一点的极坐标为
则点在圆上,故,
所以的极坐标方程为()
(Ⅱ),两点的极坐标分别为,,
又因为
所以
故,所以或
24.证明:(Ⅰ)∵
∴
又∵
由题中条件知
∴
即
(Ⅱ)∵
同理:,
∴
∴
∴