江苏省南通市2020届高三高考考前模拟卷数学试题（十）含附加题 含答案 8页

高三数学（I 卷） 第 1 页（共 4 页） 南通市 2020 届高考考前模拟卷（十） 数 学Ⅰ （南通数学学科基地命题） 一、填空题:本大题共 14 小题,每小题 5 分,共 70 分．请把答案直接填写在答题卡相应位置上．．．．．．．．. 1．若集合 { | 2 4}, { | }A x x B x x a   ≤ ，若 { | 3 4}A B x x   ，则实数 a  ▲ . 2．设复数 z＋1 z－1＝－i，其中 i 为虚数单位，则||z  ▲ . 3. 根据如图所示的伪代码，当输出 y 的值为 1 时， 则输入的 x 的值为 ▲ . 4. 在等比数列{an}中，a1＋a2=1，a5＋a6=16， 则 a9＋a10= ▲ . 5. 已知双曲线 x2－y2 =1，则其两条渐近线的夹角为 ▲ . 6．设实数 x，y 满足条件 0 1, 0 2, 2 1, x y yx     ≤ ≤ ≤ ≤ ≥ 则| 3 4 3|xy的 最大值为 ▲ . 7．若函数 sin( )( 0)yx     的部分图象如图所示， 则 的值为 ▲ . 8. 设集合 B 是集合 A=(1，2，3，4}的子集，若记事件 M 为:“集合 B 中的元素之和为 5”，则事件 M 发生的概率为 ▲ . 9. 若函数 f(x)=2cos(x+2θ)+ cos2x (0<θ<π 2)的图象过点 M(0，1)，则 f(x)的值城为 ▲ . 10. 设函数 f(x)=x3 +ax2 +bx+c 的三个零点 x1，x2，x3 是公差为 1 的等差数列，则 f(x)的极小 值为 ▲ . 11. 在△ABC 中，AB=8，AC=6，A=60°，M 为△ABC 的外心，若AM→ =λAB→+μAC→，λ、μ∈R， 则 4λ＋3μ＝ ▲ . 12. 已知△ABC 的面积等于 1，若 BC=1，当三边之积取得最小值时，则 sinA= ▲ . x y y0 11π 24 y0 5π 24 O （第 8 题图） （第 3 题图） Read x If x ≤0 Then y ←x2＋1 Else y ← lnx End If Print y 高三数学（I 卷） 第 2 页（共 4 页） 13. 已知 F 是椭圆 C: x2 a2＋y2 b2＝1(a＞b＞0)的一个集点，P 是椭圆 C 上的任意一点，则 PF 称 为椭圆 C 的焦半径.设椭圆 C 的左顶点与上顶点分别为 A，B，若存在以 A 为圆心，PF 长为半径的圆经过点 B，则椭圆 C 的离心率的最小值为 ▲ . 14. 已知 f(x) = acosx－4cos3 x，若对任意的 x∈R，都有|f(x)|≤1，则 a= ▲ . 二、解答题：本大题共 6 小题，共 90 分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字 说明、证明过程或演算步骤． 15.（本小题满分 14 分） 已知函数 f(x) = sin(ωx+φ) (ω>0，|φ|＜π 2)的图象关于直线 x＝π 6对称，两个相邻的最高点 之间的距离为 2π． (1) 求函数 f(x)的解析式; (2) 在△ABC 中，若 f (A)=一3 5，求 sinA 的值． 16.（本小题满分 14 分） 如图在平行六面体 ABCD-A1B1C1D1 中，底面 ABCD 为菱形，E 为 CC1 的中点， 平面 AA1C1C⊥平面 A1B1C1D1， 证明: (1) A1C∥平面 B1D1E; (2) 平面 AA1C1C⊥平面 B1D1E (第 16 题图) A C A1 B1 C1 D1 D E B 高三数学（I 卷） 第 3 页（共 4 页） 17.（本小题满分 14 分） 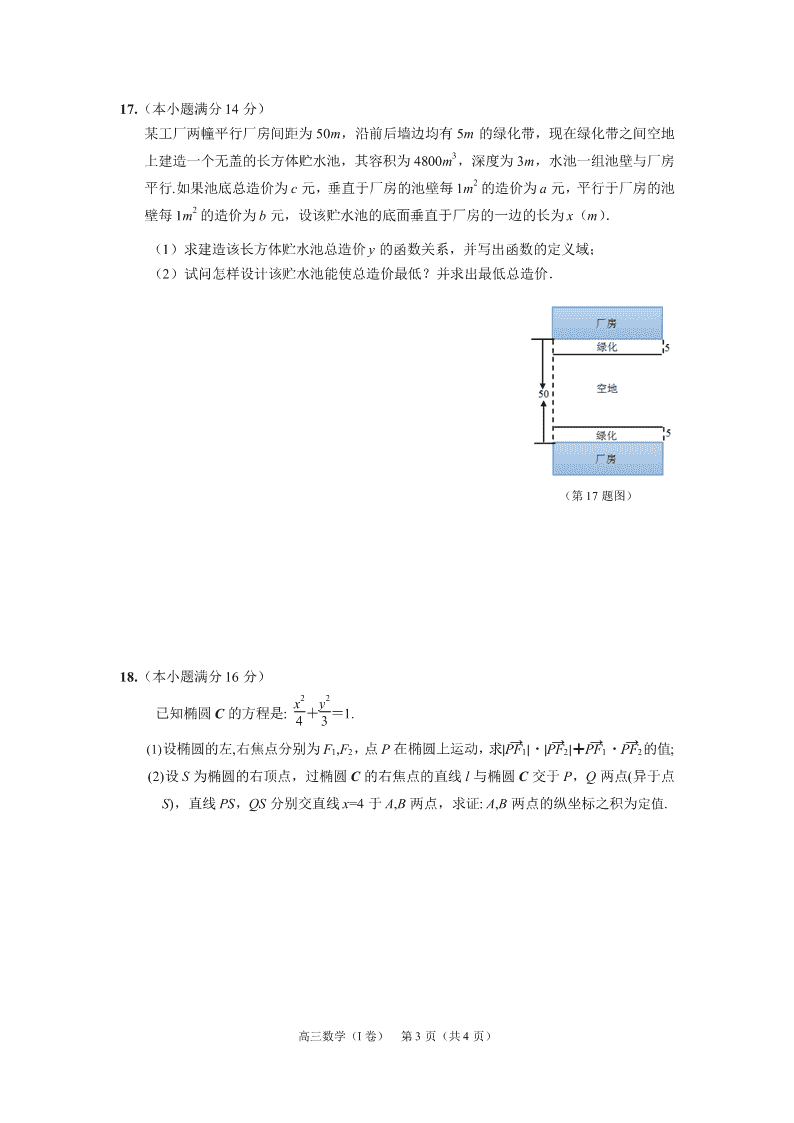某工厂两幢平行厂房间距为 50m，沿前后墙边均有 5m 的绿化带，现在绿化带之间空地 上建造一个无盖的长方体贮水池，其容积为 4800m3，深度为 3m，水池一组池壁与厂房 平行.如果池底总造价为 c 元，垂直于厂房的池壁每 1m2 的造价为 a 元，平行于厂房的池 壁每 1m2 的造价为 b 元，设该贮水池的底面垂直于厂房的一边的长为 x（m）． （1）求建造该长方体贮水池总造价 y 的函数关系，并写出函数的定义域； （2）试问怎样设计该贮水池能使总造价最低？并求出最低总造价． 18.（本小题满分 16 分） 已知椭圆 C 的方程是: x2 4＋y2 3＝1. (1)设椭圆的左,右焦点分别为 F1,F2，点 P 在椭圆上运动，求|PF1 → |・|PF2 → |＋PF1 → ・PF2 → 的值; (2)设 S 为椭圆的右顶点，过椭圆 C 的右焦点的直线 l 与椭圆 C 交于 P，Q 两点(异于点 S)，直线 PS，QS 分别交直线 x=4 于 A,B 两点，求证: A,B 两点的纵坐标之积为定值. （第 17 题图） 高三数学（I 卷） 第 4 页（共 4 页） 19.（本小题满分 16 分） 已知等差数列{an}的前 n 项和为 Sn，且 Sn =1 2n 2 +1 2n+a，数列{bn}满足 b2 n-1= a2 n-1 (n∈N*)， 且对任意正整数 m，使得 b2 m，b2 m +1，b2 m +2，…，b2 m+1 成等比数列,公比为 qm. (1) 求 a 的值; (2) 求数列{qn}的前 n 项积 Tn； (3) 记数列{bn}的前 n 项和为 Bn，求证: Sn≥Bn. 20.（本小题满分 16 分） 已知函数 f(x)＝ex－a 2x2，（ a＞0），其中 e 为自然对数的底数. (1)∀x1，x2∈R，x1≠x2，均有ex2－ex1 x2－x1 ＞m，求实数 m 的取值范围； (2) ① 设曲线 y= f(x)在 x=Ina 处的切线为直线 l，求曲线 y= f(x)与直线 l 的公共点的个数; ② 求证: 存在唯一的 x0∈R，使得对任意的 x1∈(－∞，x0)且 x2∈(x0，+∞)，均有 f(x2)－f(x1) x2－x1 ＞f′(x0). 高三数学 II（附加题） 第 1 页（共 1 页） 南通市 2020 届高考考前模拟卷（十） 数学Ⅱ(附加题) 21．【选做题】本题包括 A、B、C 三小题，请选定其中两小题．．．．．．．．，并在相应的答题区域内作答．．．．．．．．．．．．， 若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤． A．[选修 4－2：矩阵与变换]（本小题满分 10 分） 已知矩阵 M= 1 3 －1 0 ，N=    1 2 1 0 2 ，求矩阵 AB 的逆矩阵(AB)-1 B．[选修 4－4：坐标系与参数方程]（本小题满分 10 分） 在平面直角坐标系 xOy 中，已知直线 l：  x＝t， y＝－2＋kt (t 是参数，k 是实数)，曲线 C1 的方 程为  x＝2cosθ， y＝sinθ (θ 为参数)，若直线 l 与曲线 C1 无公共点，求实数 k 的取值范围. C．[选修 4－5：不等式选讲]（本小题满分 10 分） 若关于 x 的不等式 2|x－a|＋|x|≥2x－3 恒成立，求实数 a 的取值范围. 【必做题】第22 题、第23 题，每题10 分，共计20 分．请在答题卡指定区域．．．．．．．内作答，解答时应写 出文字说明、证明过程或演算步骤． 22．（本小题满分 10 分） 如图，在四核锥 P-ABCD 中，底面四边形 ABCD 为正方形， 已知 PA ⊥平面 ABCD，AB=2，PA = 2. (1) 求 PC 与平面 PBD 所成角的正弦值; (2) 在棱 PC 上是否存在一点 E，使得平面 BDE⊥平面 PBD. 若存在，求PE PC的值若不存在，请说明理由. 23．（本小题满分 10 分） 请先阅读:对于组合恒等式 Cm n = Cn-m n 我们可以例设一个情境来解释:一方面，可以从 n 个元素 中选择其中 m 个元素；另一方面，也可以从 n 个元素中别除 n－m 个元素，留下剩余的部分 运用“算两次”的方法，原恒等式成立. (1) 请尝试创设一个情境，解释恒等式: kCk n=n Ck-1 n-1 (2) 在集合 A=(1，2，3，…，3n(n≥2，n∈N*)中,随机选择其中 n 个元素，组成集合 A 的一 个子集 M，设集合 M 中能被 3 整除的元素个数记为随机变量 X，证明:随机变量 X 的数 学期望 E(X)=n 3. P A B C D E 高三数学参考答案 第 1 页（共 2 页） 南通市 2020 届高考考前模拟卷（十） 试题Ⅰ参考答案(详细答案见教参) 一、填空题：本大题共 14 小题，每小题 5 分，共 70 分． 1、答案：3 参考解答或提示:因为 { | 4}A B x a x   ={ | 3 4}xx ，所以a  3. 2、答案：1 参考解答或提示:化简得 1i 1iz   ，所以||z  1. 3、答案： 0 或 e 4、答案： 256 5、答案：90° 6、答案：14 参考解答或提示:画出可行域（如图）， 可知 0, 0xy， 所以目标函数 | 3 4 3| 3 4 3z x y x y      在点 1,2A（ ）处取得最大值 14. 7、答案：4 参考解答或提示:由图可知11 5 24 24   ，所以 =4 . 8、答案：1 8 9、答案：[-3，3 2] 10、答案：－ 2 3 9 11、答案：7 3 12、答案： 8 17 13、答案：－1＋ 3 2 14、答案：3 二、解答题（共 90 分） 15、（本小题满分 14 分） （1）f(x) = sin(x+π 3)； （2）4 3－3 4 . 16、（本小题满分 14 分） （略,见图） 17、（本小题满分 14 分） （1）y=c＋6(ax+1600b x )，x∈（0，40]; (第 16 题图) A C A1 B1 C1 D1 D E B 高三数学参考答案 第 2 页（共 2 页） （2）当 b≤a 时，水池设计成垂直于厂房的一边的边长为 40 b am，平行于厂房的一边的 边长为 40 a b的长方形时，造价最低为(c+480 ab)元; 当 b>a 时，水池设计成底面边长为 40m 的正方形时，造价最低为(c+240a+240b)元. 解（1）由题意，贮水池的底面垂直于厂房的一边长为 x m， 则平行于厂房的一边长为 4800 m3x ，即 1600 mx ， 所以总造价 16002 3 2 3y c a x b x        ，即  16006 0,40 .by c a x xx       ， （2）因为 0, 0ab，所以 1600 16002 80 .bba x ax abxx   ≥ 当且仅当 1600 ,bax x 即 40 bx a 时取等号. 若 ba≤ ,则 40 0,40b a  ,当 40 bx a 时, min 480y c ab ； 若 ba ,则当  0,40x 时, 2 22 1600 16006 6 0b ax byaxx        ， 所以函数 y 在 x∈(0,40]上单调递减，也即当 x＝40 时， min 240 240y c a b   . 综上可知，当ba≤ 时，水池设计成垂直于厂房的一边的边长为 40 mb a ，平行于厂房的一 边的边长为 40 ma b ，最低造价为 480c ab 元；当ba 时，水池设计成底面边长为 40m 18、（本小题满分 16 分） （1）6; （2）定值为－9. 19、（本小题满分 16 分） （1）a=0;（2）Tn=21－ 1 2n（3）（略） 20、（本小题满分 16 分） （1）（－∞，0]; （2）（略） 高三数学参考答案 第 3 页（共 2 页） 数学Ⅱ(附加题) 21．【选做题】本题包括 A、B、C 三小题，请选定其中两小题．．．．．．．．，并在相应的答题区域内作答．．．．．．．．．．．．， 若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤． A．[选修 4－2：矩阵与变换]（本小题满分 10 分） 答案：(AB)-1=      －1 3 － 7 3 1 6 1 6 B．[选修 4－4：坐标系与参数方程]（本小题满分 10 分） 答案：(－ 3 2 ， 3 2 ) C．[选修 4－5：不等式选讲]（本小题满分 10 分） 答案：（－∞，3]; 【必做题】第22 题、第23 题，每题 10 分，共计20 分．请在答题卡指定区域．．．．．．．内作答，解答时应写 出文字说明、证明过程或演算步骤． 22．（本小题满分 10 分） （1） 10 10 ; （2）2 3. 23．（本小题满分 10 分） （略）