江苏省昆山市2020届高三数学全国统一考试密卷1（Word版附答案） 10页

1 江苏省昆山市 2020 届普通高等学校招生全国统一考试（柏高密卷 1） 数学试卷 一、填空题（本大题共 14 小题，每小题 5 分，共 70 分，请将答案填写在答题卷相应的位置 上．） 1．已知集合 A＝{0，1，4}，B＝{﹣2，0，2，4}，则 A  B＝ ． 2. 已知复数 3 i 1 iz   ，其中 i 为虚数单位，则复数 z 的模是 ． 3．抛物线 2 16y x 的准线方程为 ． 4．某市为了响应江苏省“农村人居环境整治的新实践”，调研农村环境整治情况，按地域将 下辖的 250 个行政村分成 A，B，C，D 四组，对应的行政村个数分别为 25，75，100， 50，若用分层抽样抽取 50 个行政村，则 B 组中应该抽取的行政村数为 ． 5．执行如图所示的程序框图，输出的 S 的值为 ． 6. 中国古典乐器一般按“八音”分类，在《周礼·春官·大师》中按乐 器的制造材料对乐器分类，分别为“金、石、木、土、革、丝、范、 竹”八音，其中“土、响、 竹”为吹奏乐器，“金、石、木、革”为 打击乐器，“丝”为弹拨乐器．现从“八音”中任取不同的“一音”， 则不是吹奏乐器的概率为 ． 7．已知函数 2log (3 ), 0 ( ) 3 , 02 x x f x x x      ，若 1( ) 2f a  ，则实数 a 的值 是 ． 8．已知 na 和 nb 均为等差数列，若 2 7 6a b  ， 4 5 9a b  ，则 6a 3b 的值是 ． 9．已知 1x ， 2x 为函数 ( ) e sinxf x x 的两个极值点，则 1 2x x 的最小值为 ． 10．在长方体 ABCD—A1B1C1D1 中，AB＝4，AD＝4，AA1＝3，若在长方体中挖去一个体 积最大的圆柱，则此圆柱与原长方体的体积比为 ． 11．在平面直角坐标系 xOy 中，已知圆 C： 2 2( 3) ( 4) 16x y    ，若对于直线 1 0x my   上的任意一点 P，在圆 C 上总存在 Q 使∠PQC＝ 2  ，则实数 m 的取值范围为 ． 12．如图，在平行四边形 ABCD 中，AB＝3，AD＝2，∠BAD＝ 3  ，E 为 BC 的中点，若线段 DE 上存在一点 M 满足 AM  ＝ 1 AB AD3 m  (mR)，则 AM BD  的值是 ． 13．在△ABC 中，设角 A，B，C 对应的边分别为 a，b，c，记△ABC 的面积为 S，若 tanA ＝2tanB，则 2 S a 的最大值为 ． 2 14．已知函数 3( ) 3f x x ax  (a＞0)，其图象记为曲线 C，曲线 C 上存在异于原点的点 P， 使得曲线 C 与其在 P0 的切线交于另一点 P1，曲线 C 与其在 P1 的切线交于另一点 P2， 若直线 P0P1 与直线 P0P2 的斜率之积小于﹣9，则 a 的取值范围为 ． 二、解答题（本大题共 6 小题，共计 90 分，请在答题纸指定区域内作答，解答时应写出文 字说明、证明过程或演算步骤．） 15．（本小题满分 14 分） 已知平面向量 a  ＝(2cos ，1)，b  ＝(1，3sin )． （1）若 a  ∥b  ，求 sin2 的值； （2）若 a  ⊥b  ，求 tan( ＋ 4  )的值． 16．（本小题满分 14 分） 如图，在三棱锥 P—ABC 中，BC⊥平面 PAB，已知 PA＝AB，D，E 分別为 PB，BC 的中点． （1）求证：AD⊥平面 PBC； （2）若点 F 在线段 AC 上，且 AF 1 FC 2  ，求证：AD∥平面 PEF． 3 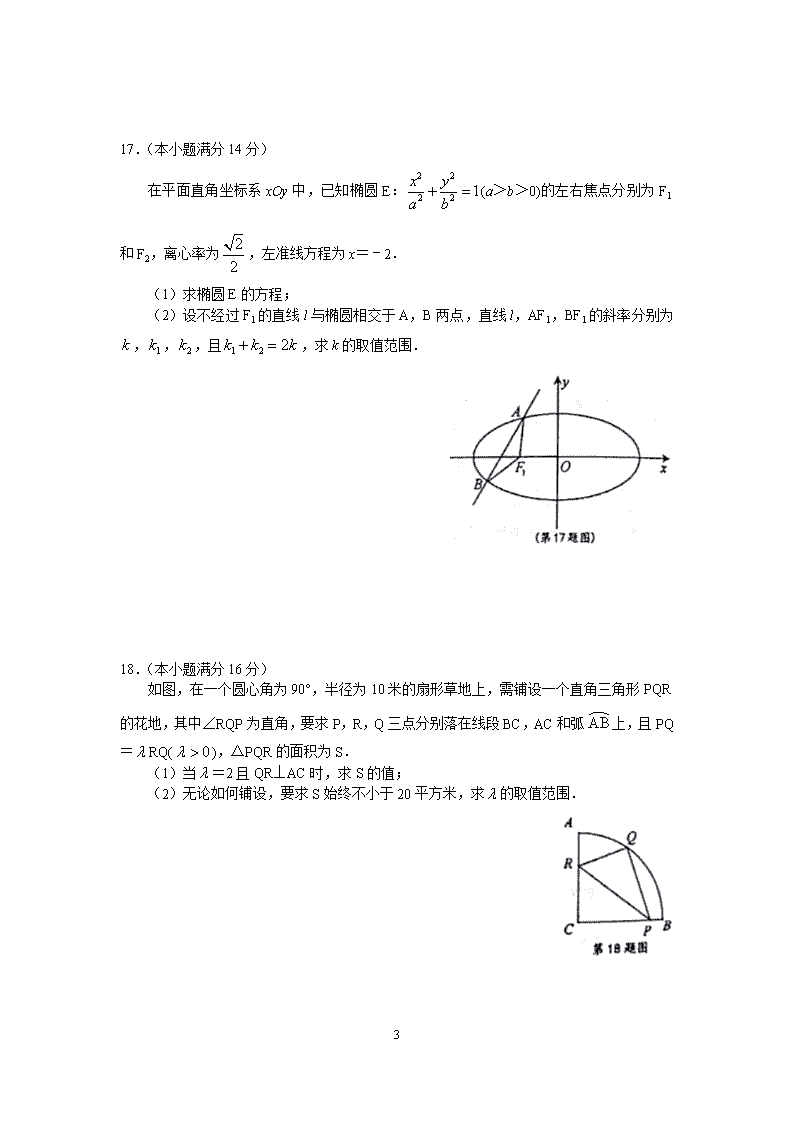17．（本小题满分 14 分） 在平面直角坐标系 xOy 中，已知椭圆 E： 2 2 2 2 1x y a b   (a＞b＞0)的左右焦点分别为 F1 和 F2，离心率为 2 2 ，左准线方程为 x＝﹣2． （1）求椭圆 E 的方程； （2）设不经过 F1 的直线 l 与椭圆相交于 A，B 两点，直线 l，AF1，BF1 的斜率分别为 k ， 1k ， 2k ，且 1 2 2k k k  ，求 k 的取值范围． 18．（本小题满分 16 分） 如图，在一个圆心角为 90°，半径为 10 米的扇形草地上，需铺设一个直角三角形 PQR 的花地，其中∠RQP 为直角，要求 P，R，Q 三点分别落在线段 BC，AC 和弧 AB 上，且 PQ＝  RQ( 0  )，△PQR 的面积为 S． （1）当  ＝2 且 QR⊥AC 时，求 S 的值； （2）无论如何铺设，要求 S 始终不小于 20 平方米，求  的取值范围． 4 19．（本小题满分 16 分） 已知在每一项均不为 0 的数列 na 中， 1 3a  ，且 1n n n ta pa a   （p，t 为常数，n N ）， 记数列 na 的前 n 项和为 nS ． （1）当 t＝0 时，求 nS ； （2）当 p＝ 1 2 ，t＝2 时，①求证：数列 2lg 2 n n a a      为等比数列；②是否存在正整数 m， 使得不等式 2nS n m  对任意 n N 恒成立？若存在，求出 m 的最小值；若不存在，请说 明理由． 20．（本小题满分 16 分） 定义：函数 ( )f x 的导函数为 ( )f x ，函数 ( )f x 的导函数为 ( )f x ，我们称函数 ( )f x 称为函数 ( )f x 的二阶导函数．已知 2( ) e ( 3)xp x x  ， ( ) e 2xq x ax   ． （1）求函数 ( )p x 的二阶导函数； （2）已知定义在 R 上的函数 ( )g x 满足：对任意 xR， ( )g x ＞0 恒成立．P 为曲线 ( )y g x 上的任意一点．求证：除点 P 外，曲线 ( )y g x 上每一点都在点 P 处切线的上方； （3）试给出一个实数 a 的值，使得曲线 ( )y p x 与曲线 ( )y q x 有且仅有一条公切线， 并证明你的结论． 5 6 7 8 9 10