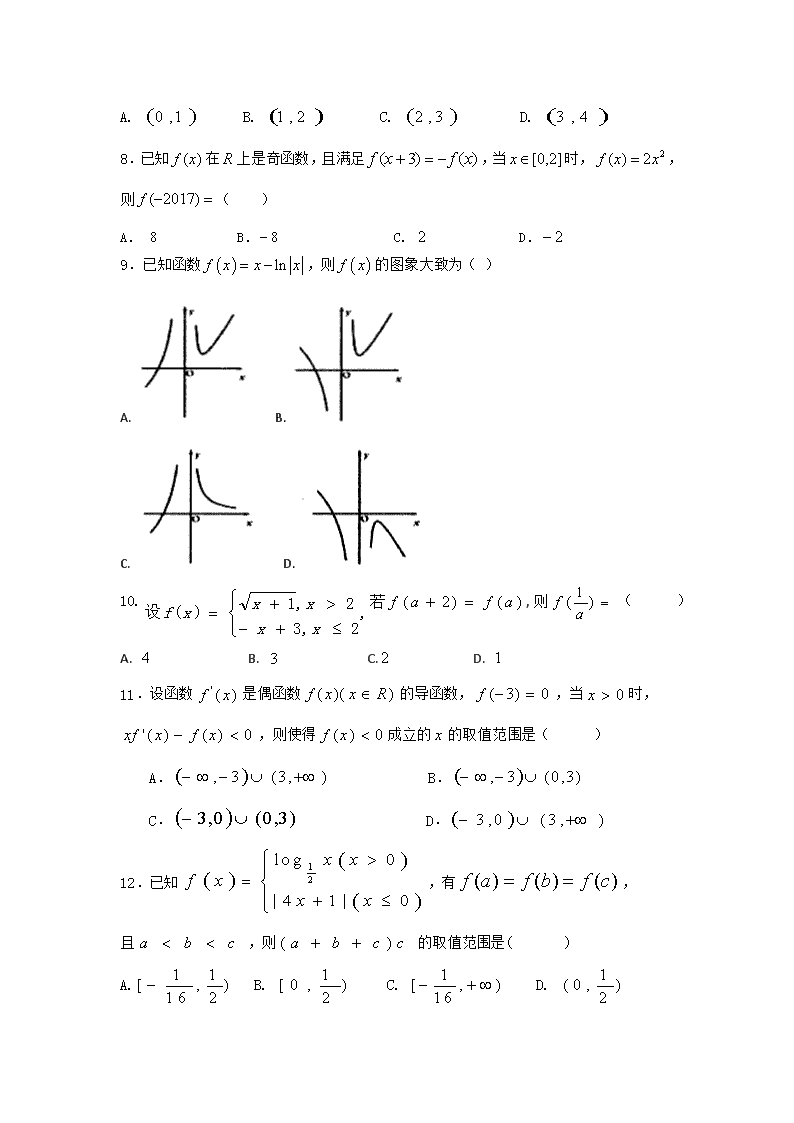- 493.50 KB
- 2023-12-27 发布
福州市八县(市)协作校2016-2017学年第二学期期末联考
高二文科 数学试卷
【完卷时间:120分钟;满分:150分】
命题:福清融城中学 林厚栋 薛从琛
一、选择题(本题共12小题,每小题5分,共60分,只有一个选项正确,请把答案写在答题卷上)
1.已知集合A={1,2,3,4},,则A∩B= ( )
A.{1,4} B.{2,3} C.{9,16} D.{1,2}
2.下列函数中,定义域相同的函数是( )
A. B. C. D.
3.下列命题为真命题的是 ( )
A.命题:“若,则” 的否命题是:“若,则”.
B.
C.命题:,
D.命题: “,使得”的否定是: “”.
4.函数必过定点( )
A.(1,0) B. (0,1) C.(3,-1) D.(4,-2)
5.已知函数,则( )
A. B. C. D.
6.已知,则的大小关系为( )
A. B. C. D.
7.( )
A. B. C. D.
8.已知在上是奇函数,且满足,当时,,则( )
A. B. C. D.
9.已知函数,则的图象大致为( )
A. B.
C. D.
10.,( )
A. B. C. D.
11.设函数是偶函数的导函数,,当时,,则使得成立的的取值范围是( )
A. B.
C. D.
12.已知,有,
且,则的取值范围是( )
A. B. C. D.
二、填空题(本题共4小题,每小题5分,共20分,请把答案写在答题卷上)
13.已知,,则________.
14.曲线 在点(1,1)处的切线方程为_______________.
15. 已知集合有且只有一个元素,则实数a的值为_______________.
16. 已知函数,曲线上存在两个不同的极值点,则实数的取值范围是__________.
三、 解答题(本题共6个小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤,请把答案写在答题卷上)
17. (本小题满分10分)
已知全集,集合,集合
(Ⅰ)求
(Ⅱ),若求实数取值范围.
18. (本小题满分12分)
命题:,命题:,若为假命题,为真命题,求实数m的取值范围.
19.(本小题满分12分)已知函数,
(1) 求函数的定义域并判断其奇偶性。
(2) 求不等式的解集.
20. (本小题满分12分)某货轮匀速行驶在相距300海里
的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比;当航行速度为30海里/小时时,每小时的燃料费用为450元,其他费用为每小时800元,且该货轮的最大航行速度为50海里/小时.
(1) 请将从甲地到乙地的运输成本(元)表示为航行速度(海里/小时)
的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
21.(本小题满分12分)已知函数
(1)若f(x)在(﹣∞,+∞)上不单调,试判断的大小关系;
(2)若f(x)在x=1时取得极值为,且时,恒成立,求的取值范围.
22. (本小题满分12分)已知函数
(1)当a为何值时,曲线在x=1处的切线与y轴垂直;
(2)讨论f(x)的单调性;
(3)当a<0时,试证明
福州市八县(市)协作校2016-2017学年第二学期期末联考
高二数学文科参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
B
C
A
B
C
D
A
C
A
B
二、填空题:
13. 14.2x-y-1=0(写成y=2x-1也得分) 15.0或4 16.
三、解答题:
17.解:(Ⅰ) ……2分
=……4分
……6分
(Ⅱ),
……8分
结合数轴可知
. ……10分
18.
解:由:得; ……2分
又:得,∴……4分
又因为为假命题,为真命题,
所以、中必然一真一假,……5分
……8分
……11分
所以,满足题意的m的取值范围是……12分
19. (本小题12分)
……2分
……3分
……4分
……8分……12分
20.(本小题12分)
解:(1)由题意,每小时的燃料费用为,当x=30时,900k=450,解得k=0.5……2分
从甲地到乙地所用的时间为小时,则从甲地到乙地的运输成本, ……5分
故所求的函数为 ……6分
法一:……8分
(x=-40舍去)
……10分
因此当x=40时,y取得极小值,也是最小值。……11分
故当货轮航行速度为40海里/小时时,能使该货轮运输成本最少.……12分
法二(2)由(1)得 ,……9分
当且仅当,即时取等号.……11分
故当货轮航行速度为40海里/小时时,能使该货轮运输成本最少.……12分
21.(本小题12分)
(1)(2)(﹣∞,﹣1)∪(2,+∞)
解:(1)f′(x)=3x2﹣2ax+b,∵f(x)在(﹣∞,+∞)是不单调函数,开口向上
∴f′(x)=0有两个不同的实数根,∴△=,可得 ……4分
(2)由题意可得,解得∴f′(x)=3x2﹣x﹣2,……6分
列表分析最值:
x
-1
(-1, )
(,1)
1
(1,2)
2
f(x)
+
0
-
0
+
+c
递增
极大值+c
递减
极小值+c
递增
2+c
∴当x∈[﹣1,2]时,f(x)的最大值为f(2)=2+c,……10分
∵对x∈[﹣1,2]时,f(x)<c2恒成立,∴c2>2+c,解得c<﹣1或c>2,
故c的取值范围为(﹣∞,﹣1)∪(2,+∞) ……12分
考点:学生没有列表,理由充分也可得分。
22. (本小题12分)
……1分
(2)……4分
当时,,则在单调递增……5分
当时,则在单调递增,在单调递减.…… 7分
(3)由(2)知,当时,…… 8分
,令 ()
则,解得…… 10分
∴在单调递增,在单调递减…… 11分
∴,∴,即,∴.
… 12分