2013届人教A版文科数学课时试题及解析（58）随机数与几何概型 4页

课时作业(五十八)　[第58讲　随机数与几何概型]‎ ‎ [时间：35分钟　　分值：80分]‎ ‎1．在集合{1,2,3,4,5,6,7,8,9}中产生一个均匀随机数，则得到数字8的概率是(　　)‎ A. B. C. D. ‎2．容量为400 ml的培养皿里装满培养液，里面有1个细菌，从中倒出20 ml的培养液，则细菌被倒出的概率是(　　)‎ A. B. C. D. ‎3．点A为周长等于3的圆周上的一个定点，若在该圆周上随机取一点B，则劣弧AB的长度小于1的概率为(　　)‎ A. B. C. D. ‎4． 在边长为1的正方形ABCD内随机选一点M，则点M到点D的距离小于正方形的边长的概率是________．‎ ‎5．在等腰Rt△ABC中，在斜边AB上任取一点M，则AM的长小于AC的长的概率是(　　)‎ A. B. C. D. ‎6． 在区间(0，π]上随机取一个数x，则事件“sinx＋cosx≤‎1”‎发生的概率为(　　)‎ A. B. C. D. 图K58－1‎ ‎7． 如图K58－1所示，墙上挂有边长为a的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为的圆弧围成的，某人向此板投镖，假设每次都能击中木板，且击中木板上每个点的可能性都一样，则它击中阴影部分的概率是(　　)‎ A. B．1－ C．1－ D．与a的取值有关 ‎8． 在区间[－π，π]内随机取两个数分别记为a，b，则使得函数f(x)＝x2＋2ax－b2＋π2有零点的概率为(　　)‎ A．1－ B．1－ C．1－ D．1－ ‎9．将一条‎4米长的绳子随机地截成两条，用A表示所截两段绳子都不短于‎1米的事件，则事件A发生的概率是________．‎ ‎10． 一只蚂蚁在边长分别为3,4,5的三角形的边上爬行，某时刻该蚂蚁距离三角形的三个顶点的距离均超过1的概率是________．‎ ‎11．某人欲从某车站乘车出差，已知该站发往各站的客车均每小时一班，则此人等车时间不多于10分钟的概率为________．‎ ‎12．(13分) 某班主任统计本班50名学生放学回家后学习时间的数据，用条形图表示(‎ 如图K58－2)．‎ ‎(1)求该班学生每天在家学习时间的平均值；‎ ‎(2)该班主任用分层抽样方法(按学习时间分五层)选出10个学生谈话，求在学习时间为1个小时的学生中选出的人数；‎ ‎(3)假设学生每天在家学习时间为18时至23时，已知甲每天连续学习2小时，乙每天连续学习3小时，求22时甲、乙都在学习的概率．‎ 图K58－2‎ ‎13．(12分)设有关于x的一元二次方程x2＋2ax＋b2＝0.‎ ‎(1)若a是从0,1,2,3四个数中任取的一个数，b是从0,1,2三个数中任取的一个数，求上述方程有实根的概率；‎ ‎(2)若a是从区间[0,3]任取的一个数，b是从区间[0,2]任取的一个数，求上述方程有实根的概率．‎ 课时作业(五十八)‎ ‎【基础热身】‎ ‎1．A　[解析] 依据均匀随机数的概念知，在该集合内得到任何一个整数的概率都是.故选A.‎ ‎2．B　[解析] 细菌被倒出的概率为P＝＝，故选B.‎ ‎3．C　[解析] 点B可以在点A的两侧来取，距离点A的最远处时，AB的弧长为1，根据几何概率可知其整体事件是其周长3，则其概率是.故选C.‎ ‎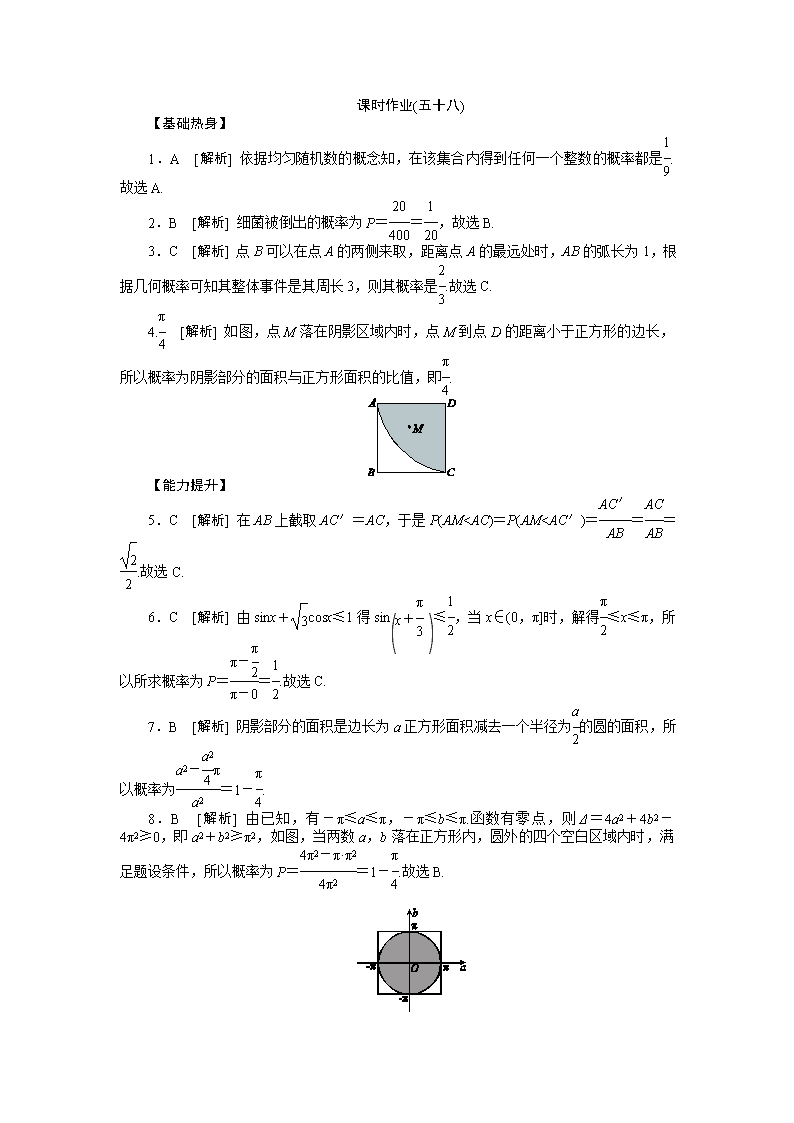4.　[解析] 如图，点M落在阴影区域内时，点M到点D的距离小于正方形的边长，所以概率为阴影部分的面积与正方形面积的比值，即.‎ ‎【能力提升】‎ ‎5．C　[解析] 在AB上截取AC′＝AC，于是P(AM