- 1.96 MB
- 2023-12-24 发布
程溪中学2016-2017学年上学期期末考
高二文科数学试题
数据,,…,的方差其中为样本平均数
第Ⅰ卷 (选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.
1.抛物线y=2x2的准线方程是( )
A.x=- B.x= C.y=- D.y=
2、已知命题 ,,则( )
A、, B、,
C、, D、,
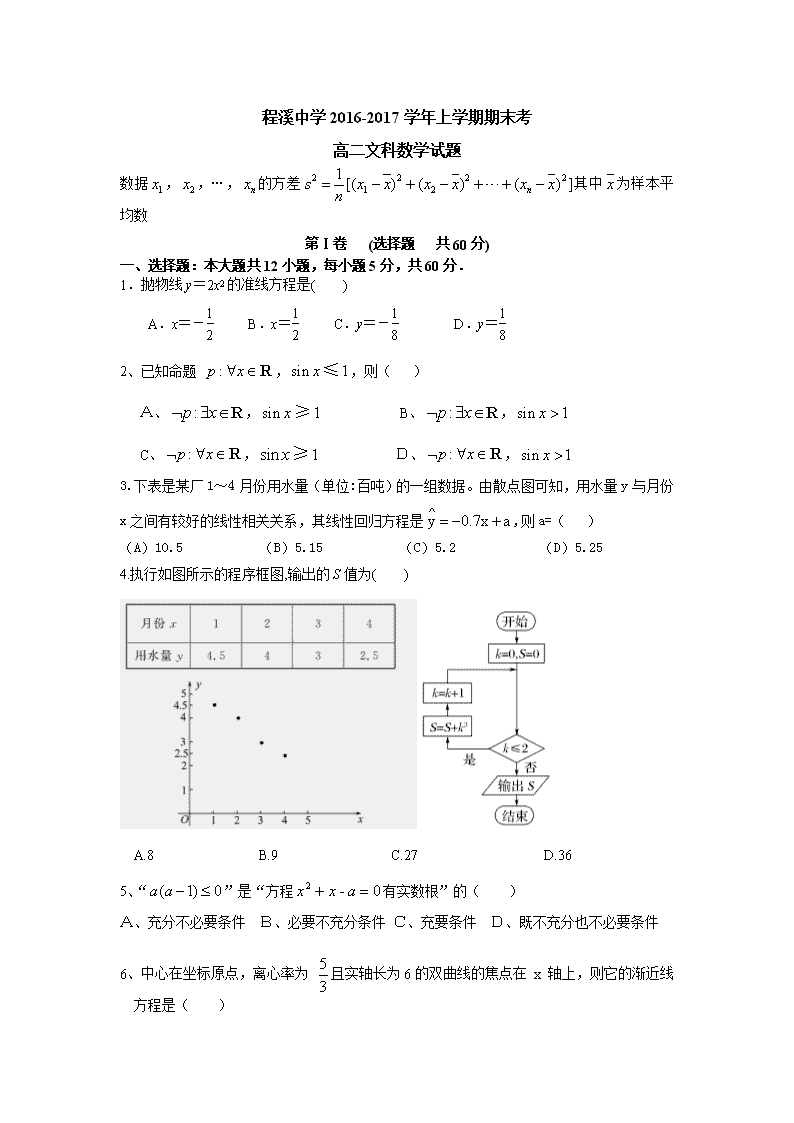
3.下表是某厂1~4月份用水量(单位:百吨)的一组数据。由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是,则a=( )
(A)10.5 (B)5.15 (C)5.2 (D)5.25
4.执行如图所示的程序框图,输出的S值为( )
A.8 B.9 C.27 D.36
5、“”是“方程有实数根”的( )
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
6、中心在坐标原点,离心率为 且实轴长为6的双曲线的焦点在 x 轴上,则它的渐近线方程是( )
A、 B、 C、 D、
7.已知抛物线y2=8x的焦点与椭圆+y2=1的一个焦点重合,则该椭圆的离心率为( )
A. B. C. D.
8、已知命题平行四边形的对角线互相平分,命题平行四边形的对角线相等,则下列命题中为真命题的是 ( )
A、 B、 C、 D、
9.下列四个命题中:
①“等边三角形的三个内角均为60°”的逆命题;
②“若k>0,则方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题;
④“若ab≠0,则a≠0”的否命题.
其中真命题的序号是________.
A ②、③ B ③、④
C ①、④ D ①、②
10设函数(x ∈R),则f ( x ) ( )
A、有最大值 B、有最小值 C、是增函数 D、是减函数
11、如图是函数 的导函数的图象,对下列四个判断:
-2 -1 0 1 2 3 4 x
y
①在(—2,—1)上是增 函数
②是极小值点
③在(—1,2)上是增 函数,在(2,4)上是减 函数
④是的 极小值点
其中正确的是( )
A、① ② B、③ ④ C、② ③ D、② ④
12.设圆锥曲线r的两个焦点分别为F1,F2,若曲线r上存在点P满=4:3:2,则曲线r的离心率等于 ( )
A. B.或2 C.2 D.
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的相应位置.
13.某单位有40名职工,现从中抽取5名职工对其体重进行统计,将全体职工随机按1~40编号,并按编号顺序平均分成5组,按系统抽样方法在各组内抽取一个号码.
(1)若第1组抽出的号码为2,则被抽出职工的最大号码为________________;
(2)分别统计这5名职工的体重(单位:kg),获得体重数据的茎叶图如图所示,则该样本的方差为________.
14.在区间[-2,4]上随机地取一个数x,若x满足x≤m的概率为,则m=________.
15.曲线y=-5ex+3在点(0,-2)处的切线方程为______________.
16、若函数在处有极大值,且对于任意恒成立,则实数的取值范围为_ _
三、解答题(共6题,满分70分)解答应写演算步骤。
17.(本小题满分10分)
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
18.(12分)(2014·安徽)某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12]
①估计该校学生每周平均体育运动时间超过4小时的概率P;
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为P,试求从中任选三人至少有一人每周平均体育运动时间超过4小时的概率
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
P(K2≥k0)
0.10
0.05
0.010
0.005
k0
2.706
3.841
6.635
7.879
附:K2=.
男生
女生
总计
每周平均体育运动时间不超过4小时
每周平均体育运动时间超过4小时
总计
19.(12分)已知中心在原点的椭圆E的左焦点F(,0),右顶点A(2,0),抛物线C焦点为A. (1)求椭圆E与抛物线C的标准方程;
(2)若过(0,1)的直线 l 与抛物线C有且只有一个交点,求直线 l的方程。
20、(12分) 已知为实数,
(1)求导数;(2)若是的极值点,求在 [ -2 ,2 ] 上的最大值和最小值;
21.(12分)已知函数f(x)=+-ln x-,其中a∈R,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=x.
(1)求a的值; (2)求函数f(x)的单调区间与极值.
F
A
B
x
y
O
P
22(12分).如图,已知抛物线 上两定点A、B分别在对称轴左、右两侧,F为抛物线的焦点,且| AF | = 2 ,| BF | = 5 。
(1)求A、B两点的坐标;
(2)在抛物线的AOB一段上求一点P,
使的面积最大,并求这个最大面积。
程溪中学2016-2017学年上学期期末考
高二文科数学答题卷
一、选择题:本大题共12小题,每小题5分,共60分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
18、
二、填空题:本大题共4小题,每小题5分,共20分
13、 14、 15、 16、
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤。
17、(本小题满分10分)
18、(本小题满分12分)
男生
女生
总计
每周平均体育运动时间不超过4小时
每周平均体育运动时间超过4小时
总计
19、(本小题满分12分)
20、(本小题满分12分)
21、(本小题满分12分)