- 408.50 KB
- 2023-11-25 发布
奉新一中2018-2019学年高二上学期第三次月考数学(文)试题
命题人:何民媛 2018.12
一、选择题:(在每小题给出的四个选项中,只有一项是符合题目要求的.本大题共12小题,每小题5分,共60分.)
1.抛物线的焦点坐标是( )
A. B. C. D.
2.命题“,”的否定是( )
A., B.,
C., D.,
3.命题“,使得”为真命题,则实数m的取值范围为( )
A.[0,4] B.(0,4) C.[-4,0) D.(-4,0)
4.a,b表示空间两条直线,为一平面,若p: a,b与平面所成角相等;q:a与b平行,则p是q( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分又不必要条件
5.设F1、F2分别是椭圆+=1的左、焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的距离为( )
A.2 B.3 C.4 D.5
6.a,b,c表示直线,M表示平面,给出下列四个命题:
①若a∥M,b∥M,则a∥b; ②若bM,a∥b,则a∥M;
③若a⊥c,b⊥c,则a∥b; ④若a⊥M,b⊥M,则a∥b.
其中正确命题的个数有( )
A.0个 B.1个 C.2个 D.3个
7.下表是某小卖部统计出的五天中卖出热茶的杯数与当天气温的对比表:
气温x(℃)
18
13
10
4
0
杯数y
24
34
39
51
62
若卖出热茶的杯数y与气温x近似地满足线性关系,则其关系式最接近的是( )
A. B. C. D.
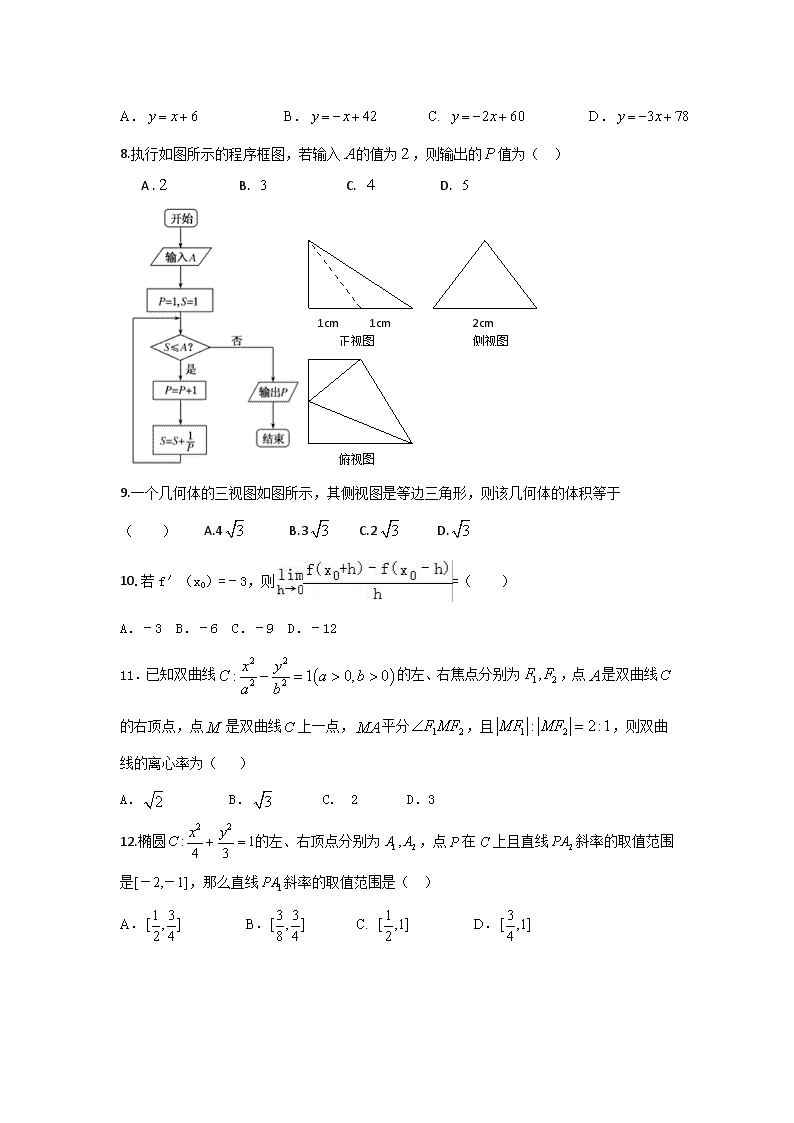
8.执行如图所示的程序框图,若输入的值为,则输出的值为( )
A . B. C. D.
1cm
1cm
2cm
正视图
侧视图
俯视图
9.一个几何体的三视图如图所示,其侧视图是等边三角形,则该几何体的体积等于 ( ) A.4 B.3 C.2 D.
10.若f′(x0)=﹣3,则=( )
A.﹣3 B.﹣6 C.﹣9 D.﹣12
11.已知双曲线的左、右焦点分别为,点是双曲线的右顶点,点是双曲线上一点,平分,且,则双曲线的离心率为( )
A. B. C. 2 D.3
12.椭圆的左、右顶点分别为,点P在C上且直线斜率的取值范围是[-2,-1],那么直线斜率的取值范围是( )
A. B. C. D.
二、填空题(本题共4小题,每小题5分,共20分)。
13.在区间[-2,3]上随机选取一个数X,则X≤1的概率为 .
14.已知双曲线()的离心率为,那么双曲线的渐近线方程为 .
15.已知P为抛物线上一个动点,定点,那么点P到点Q的距离与点P到抛物线的准线的距离之和的最小值是 .
16.已知三角形所在平面与矩形所在平面互相垂直,,
,若点都在同一球面上,则此球的表面积等于_______.
三、解答题(本大题共 6 个小题,共 70 分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.椭圆的中心为坐标原点,长、短轴长之比为,一个焦点是(0,﹣2).
(1)求椭圆的离心率; (2)求椭圆的方程.
18.已知p: “实数m满足:()”;q:“实数m满足:方程表示双曲线”;若p是q的充分不必要条件,求实数a的取值范围.
19.如图,已知直三棱柱的侧面是正方形,点是侧面的中心,,是棱的中点.
(1)求证:平面;
(2)求证:平面平面.
20.某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60)…[90,100)得到如图的频率分布直方图.
(Ⅰ)求图中实数a的值;
(Ⅱ)根据频率分布直方图,试估计该校高一年级学生其中考试数学成绩的平均数;
(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
21.如图所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S﹣AB﹣C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.
(Ⅰ)证明: BD⊥AF;
(Ⅱ)若三棱锥B﹣AEC的体积是四棱锥S﹣ABCD体积的,求点E到平面ABCD的距离.
22.已知椭圆的离心率为,若圆被直线截得的弦长为2.
(1)求椭圆的标准方程;
(2)已知点为动直线与椭圆的两个交点,问:在轴上是否存在定点,使得为定值?若存在,试求出点的坐标和定值;若不存在,请说明理由
奉新一中2020届高二上学期第三次月考数学(文)答案
命题人:何民媛 2018.12
一、选择题:(在每小题给出的四个选项中,只有一项是符合题目要求的.本大题共12小题,每小题5分,共60分.)
1.C 2.D 3.B 4.C 5.C 6.B 7 .C 8.C 9.D 10.B 11.D 12.B
二、填空题(本题共4小题,每小题5分,共20分)。
13. 14. 15. 16.
三、解答题(本大题共 6 个小题,共 70 分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.【解答】解:(1)由题意a=b,c=2,
∴=2,∴b2=,∴a=,
∴椭圆的离心率e==;
(2)椭圆的方程=1.
18.真则
真则,解得
是的充分不必要条件,则而不能推出,
19.证明:(1)略
(2) 略
20.解:(Ⅰ)由频率分布直方图,得:
10×(0.005+0.01+0.025+a+0.01)=1,
解得a=0.03.
(Ⅱ)由频率分布直方图得到平均分:
=0.05×45+0.1×55+0.2×65+0.3×75+0.25×85+0.1×95=74(分).
(Ⅲ)由频率分布直方图,得数学成绩在[40,50)内的学生人数为40×0.05=2,这两人分别记为A,B,
数学成绩在[90,100)内的学生人数为40×0.1=4,这4人分别记为C,D,E,F,
若从数学成绩在[40,50)与[90,100)两个分数段内的学生中随机选取2名学生,
则所有的基本事件有:
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),
(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15个,
如果这两名学生的数学成绩都在[40,50)或都在[90,100)内,
则这两名学生的数学成绩之差的绝对值不大于10,
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共7个,
所以这两名学生的数学成绩之差的绝对值不大于10的概率P=.
21.证明:(Ⅰ)∵四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,
二面角S﹣AB﹣C的大小为90°,
∴SA⊥AD,
又SA⊥AB,AB∩AD=A,∴SA⊥平面ABCD,
又BD⊂平面ABCD,∴SA⊥BD,
在直角梯形ABCD中,∠BAD=∠ADC=90°,
AD=2CD=1,AB=2,
∴tan∠ABD=tan∠CAD=,
又∠DAC+∠BAC=90°,
∴∠ABD+∠BAC=90°,即AC⊥BD,
又AC∩SA=A,∴BD⊥平面SAC,
∵AF⊂平面SAC,∴BD⊥AF.
解:(Ⅱ)设点E到平面ABCD的距离为h,
∵VB﹣AEC=VE﹣ABC,且=,
∴===,
解得h=,
∴点E到平面ABCD的距离为.
22.(1).圆的圆心到直线的距离,
∴,解得,又,,联立解得: ,.
∴椭圆的标准方程为: .
(2).假设在轴上存在定点,使得为定值.
设,,联立,化为,
则,,
,
令,解得.
因此在轴上存在定点使得为定值.