- 814.00 KB
- 2023-11-22 发布
绝密★启用前
眉山一中办学共同体2020届第三期10月月考试题
数学(文史类)
命题人:钟建国 审题人 陈杰
第I卷(选择题)
一、 选择题(共60分,每小题5分,每个小题有且仅有一个正确的答案)
1.直线的斜率和在轴上的截距分别是 ( )
A. B. C. D.
2.若三点A(3,1),B(-2,b),C(8,11)在同一直线上,则实数b等于( )
A.2 B.3 C.9 D.-9
3.若l、m、n是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )
A.若α∥β,l⊂α,n⊂β,则l∥n B.若α⊥β,l⊂α,则l⊥β
C.若l⊥n,m⊥n,则l∥m D.若l⊥α,l∥β,则α⊥β
4.如图,在同一直角坐标系中,直线y=ax与y=x+a表示的图像可能是( )
A. B. C. D.
5.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图
如下图所示,则这个棱柱的体积为( )
A.12 B.36
C.27 D.6
6、设是两条不同的直线, 是两个不同的平面,下列命题中错误的是( )
A、若,,,则 B、若,,,则
C、若,,则 D、若,,,则
7.已知三条相交于一点的线段PA、PB、PC
两两垂直,点P在平面ABC外,
PH⊥面ABC于H,则垂足H是△ABC的( )
A.外心 B.内心 C.垂心 D.重心
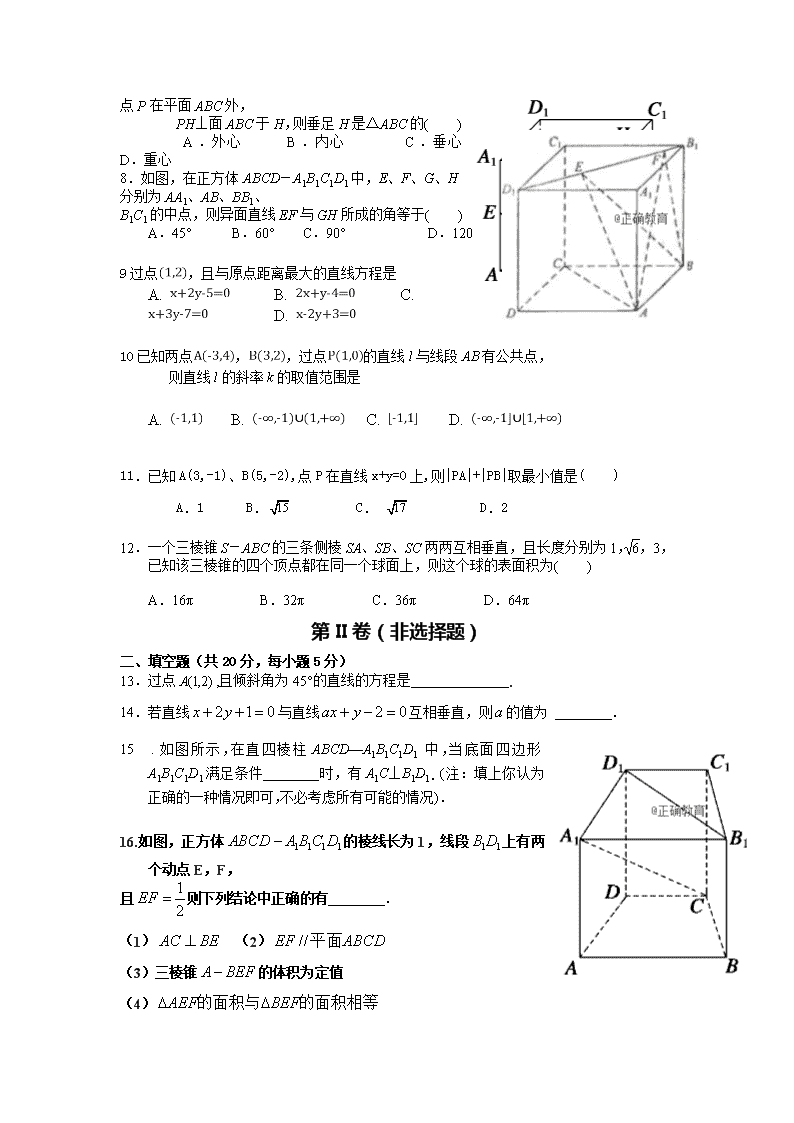
8.如图,在正方体ABCD-A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、
B1C1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60° C.90° D.120°
9过点,且与原点距离最大的直线方程是
A. B. C. D.
10已知两点,,过点的直线l与线段AB有公共点,
则直线l的斜率k的取值范围是
A. B. C. D.
11.已知A(3,-1)、B(5,-2),点P在直线x+y=0上,则|PA|+|PB|取最小值是( )
A.1 B. C. D.2
12.一个三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直,且长度分别为1,,3,
已知该三棱锥的四个顶点都在同一个球面上,则这个球的表面积为( )
A.16π B.32π C.36π D.64π
第II卷(非选择题)
二、填空题(共20分,每小题5分)
13.过点,且倾斜角为45°的直线的方程是 .
14.若直线与直线互相垂直,则的值为 .
15 .如图所示,在直四棱柱ABCD—A1B1C1D1中,当底面四边形A1B1C1D1满足条件________时,有A1C⊥B1D1。(注:填上你认为正确的一种情况即可,不必考虑所有可能的情况).
16.如图,正方体的棱线长为1,线段上有两个动点E,F,
且则下列结论中正确的有 .
(1) (2)
(3)三棱锥的体积为定值
(4)
三、解答题(共70分)
17. (本题满分10分) (10分)根据下列条件分别求出直线的方程,并化为一般式方程:
(1).直线l过点(-1,2)且与直线2x-3y+4=0平行
(2)过点P(1,1),且在x轴上的截距和在y轴上的截距相等
18(本题满分12分).△ABC的三个顶点是A(-1,4),B(-2,-1),C(2,3).
(1)求BC边的高所在直线方程;
(2)求△ABC的面积S.
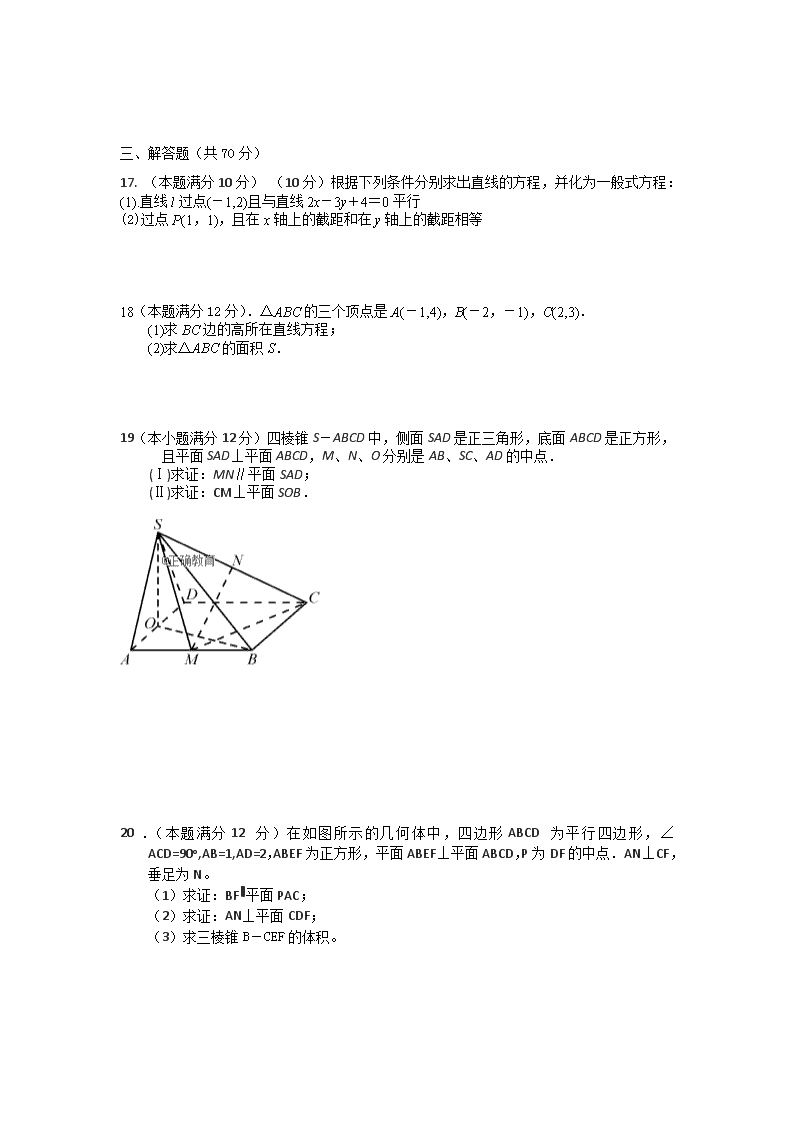
19(本小题满分12分)四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,
且平面SAD⊥平面ABCD,M、N、O分别是AB、SC、AD的中点.
(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求证:CM⊥平面SOB.
20.(本题满分12分)在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90o,AB=1,AD=2,ABEF为正方形,平面ABEF⊥平面ABCD,P为DF的中点.AN⊥CF,垂足为N。
(1)求证:BF∥平面PAC;
(2)求证:AN⊥平面CDF;
(3)求三棱锥B-CEF的体积。
21如图,菱形的对角线与交于点,点、分别在,上,,交于点,将沿折到的位置.
(Ⅰ)证明:;
(Ⅱ)若,求五棱锥体积.
22.如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF||AB,AB=2,BC=EF=1,AE=,DE=3,∠BAD=60º,G为BC的中点.
(Ⅰ)求证:FG||平面BED;
(Ⅱ)求证:平面BED⊥平面AED;
(Ⅲ)求直线EF与平面BED所成角的正弦值.
19.(12分)如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
求证:(1)直线BD1∥平面PAC;
(2)平面BDD1⊥平面PAC;
(3)直线PB1⊥平面PAC.
20. (本小题满分12分)
在三棱柱中,侧面底面,,且点为中点.
(Ⅰ)证明:平面;
(Ⅱ)求三棱锥的体积.
19. (本小题满分12分)如图,在几何体中,四边形是菱形,平面, ,且.
(1)证明:平面平面.
(2)若,求几何体的体积.
21.(12分)如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,M是线段AE上的动点.
(Ⅰ)试确定点M的位置,使AC∥平面DMF,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,且∠AED=45°,AE=,AD=CD,连接AF,求三棱锥M﹣ADF的体积.
18(本小题满分12分)
如图,正三棱柱(底面为正三角形,侧棱垂直于底面)ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
(1)求证:Al C∥平面AB1D;
(2)求点C到平面AB1D的距离.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:PA∥面BDE;平面PAC⊥平面BDE;
(2)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.
21.(12分)
已知直线l经过点P(-2,5),且斜率为-
.(1)求直线l的方程;
(2)若直线m与l平行,点P到直线m的距离为3,求直线m的方程
8
6
14.过点且在轴上截距是在轴上截距的两倍的直线的方程为 .
17.(本小题满分10分)
(1) 已知直线的方程为,直线与垂直,且过点(1,-3),求直线的方程;
(2)一个圆经过和两点,且圆心在直线
上,求圆的方程.
15.如图,某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积为________.
20.(12分)如图所示,在四棱柱(侧棱垂直于底面的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
(1)求证D1C⊥AC1;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
6. 是两个平面,是两条直线,有下列四个命题:
(1)如果,那么.(2)如果,那么.
(3)如果,那么. (4)如果,那么与所成的角和与所成的角相等.其中正确的命题个数有( )
A 1 B 2 C 3 D 4
18.
18.(12分)已知直线:,过定点P.
求定点P的坐标;
若直线与直线:平行,求k的值并求此时两直线间的距离.
19、(本小题满分12分)如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.
(Ⅰ)求证:平面DEG⊥平面CFG;
(Ⅱ)求多面体CDEFG的体积.