- 423.01 KB
- 2023-11-18 发布
2019高二下学期月考理科数学试题
一、选择题:(本大题共12小题,共60分)
1.复数( )
A. B. C. D.
2.用反证法证明命题“已知x1>0,x2≠1,且xn+1=,证明对任意正整数n,都有xn>xn+1”,其假设应为 ( )
A. 对任意正整数n,有xn≤xn+1 B. 存在正整数n,使xn>xn+1
C. 存在正整数n,使xn≤xn+1 D. 存在正整数n,使xn≥xn-1且xn≥xn+1
3.“干支纪年法”是中国历法上自古以来就一直使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸十个符号叫天干,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个符号叫地支.把干支顺序相配正好六十为一周,周而复始,循环记录,这就是俗称的“干支表”.2018年是“干支纪年法”中的戊戌年,那么2017年是“干支纪年法”中的( )
A. 丁酉年 B. 戊未年 C. 乙未年 D. 丁未年
4.复数(是虚数单位)的共轭复数在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.由y=,x=1,x=2,y=0所围成的平面图形的面积为( )
A. ln2 B. ln2-1 C. 1+ln2 D. 2ln2
6.将正整数排成下表:
则在表中数字2017出现在( )
A. 第44行第80列 B. 第45行第80列
C. 第44行第81列 D. 第45行第81列
7.函数的减区间为( )
- 4 -
A. B. C. D.
8.函数在处有极值为8,则=( )
A. -4或6 B. 4或-6 C. 6 D. -4
9.利用数学归纳法证明…且)时,第二步由到时不等式左端的变化是( )
A. 增加了这一项
B. 增加了和两项
C. 增加了和两项,同时减少了这一项
D. 以上都不对
10.已知函数在区间上单调递增,则的取值范围是( )
A. B. C. D.
11.设函数是奇函数的导函数, ,且当时, ,则使得成立的的取值范围是( )
A. B.
C. D.
12.某中学为提升学生的英语学习能力,进行了主题分别为“听”、“说”、“读”、“写”四场竞赛.规定:每场竞赛的前三名得分分别为, , (,且, , ),选手的最终得分为各场得分之和.最终甲、乙、丙三人包揽了每场竞赛的前三名,在四场竞赛中,已知甲最终分为分,乙最终得分为分,丙最终得分为分,且乙在“听”这场竞赛中获得了第一名,则“读”这场竞赛的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
二、填空题:(本大题共5小题,共25分)
13.若复数的共轭复数满足,则__________.
14.曲线在点处的切线方程为__________.
15.
- 4 -
在某班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连续出场,且女生甲不能排在第一个,那么出场顺序的排法种数为_________.
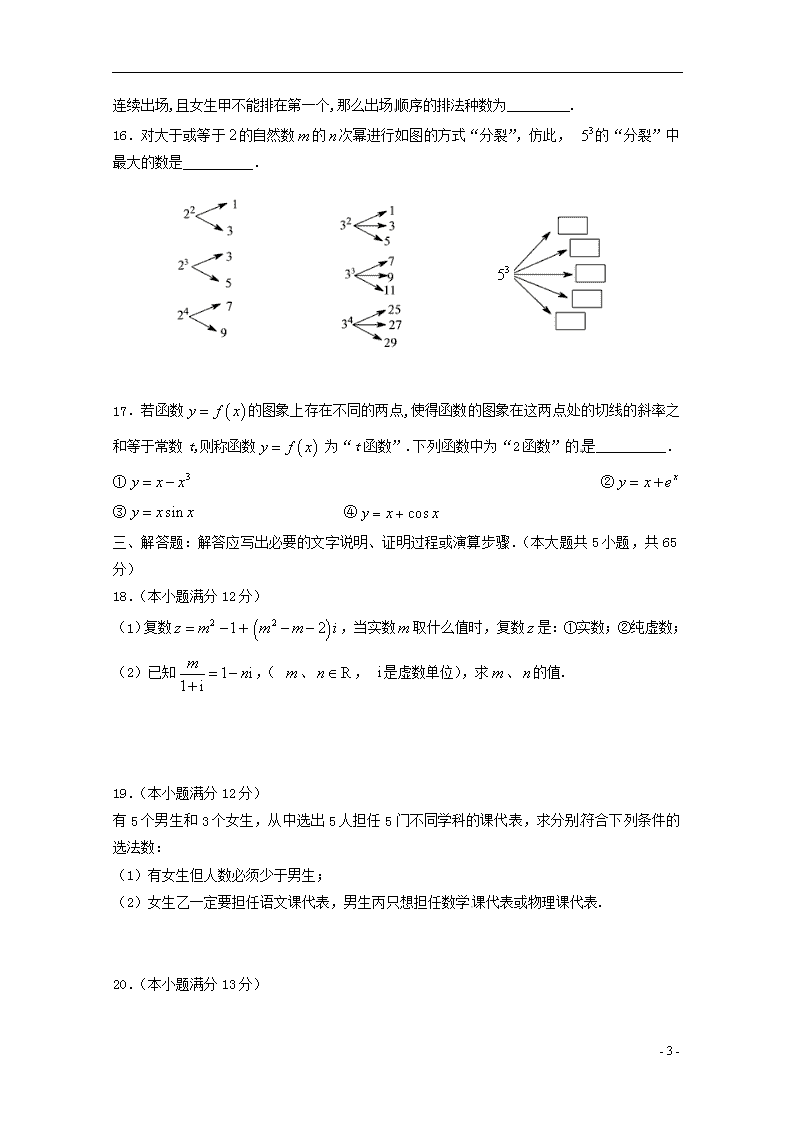
16.对大于或等于的自然数的次幂进行如图的方式“分裂”,仿此, 的“分裂”中最大的数是__________.
17.若函数的图象上存在不同的两点,使得函数的图象在这两点处的切线的斜率之和等于常数t,则称函数 为“t函数”.下列函数中为“2函数”的是__________.
① ② ③ ④
三、解答题:解答应写出必要的文字说明、证明过程或演算步骤.(本大题共5小题,共65分)
18.(本小题满分12分)
(1)复数 ,当实数取什么值时,复数是:①实数;②纯虚数;
(2)已知,( 、, 是虚数单位),求、的值.
19.(本小题满分12分)
有5个男生和3个女生,从中选出5人担任5门不同学科的课代表,求分别符合下列条件的选法数:
(1)有女生但人数必须少于男生;
(2)女生乙一定要担任语文课代表,男生丙只想担任数学课代表或物理课代表.
20.(本小题满分13分)
- 4 -
已知函数
(1)求函数的单调区间;
(2)求函数在上的最值.
21.(本小题满分14分)
已知数列的前n项和满足: ,且.
(1)求;
(2)猜想的通项公式,并用数学归纳法证明.
22.(本小题满分14分)
已知函数.
(1)当时,求曲线在点处的切线方程;
(2)讨论函数的单调区间;
(3)若函数在处取得极值,对恒成立,求实数的取值范围.
- 4 -