- 866.00 KB
- 2023-11-16 发布
华安一中2017-2018学年上学期
高二数学(理科)第二次月考试题
(考试时间:120分钟 总分:150分)
一、选择题(每题5分共60分,在每小题给出的四个选项中只有一项是符合题目要求的)
1.抛物线的准线方程是,则的值为 ( )
A.4 B.8 C. D.
2.某单位有若干名员工,现采用分层抽样的方式抽取人去体检,若老、中、青人数之比为4:1:5,已知抽到10位中年人,则样本的容量为 ( )
A. 40 B. 100 C. 80 D. 50
3.下列程序框图中,输出的的值是( )
A. B. C. D.
4.若双曲线以椭圆的焦点为顶点,以椭圆长轴的端点为焦点,则双曲线的方程为( )
A. B. C. D.
5.某小组有3名男生和2名女生,从中任选2名学生参加演讲比赛,那么下列对立的两个事件是( )
A. “至少1名男生”与“至少有1名是女生”
B. 恰好有1名男生”与“恰好2名女生”
C. “至少1名男生”与“全是男生”
D. “至少1名男生”与“全是女生”
6.已知双曲线的一条渐近线方程为,则双曲线的焦距为 ( )
A. B. C. D.
7.太极图是以黑白两个鱼形纹组成的图形图案,它形象化地表达了阴阳轮转,相反相成是万物生成变化根源的哲理,展现了一种相互转化,相对统一的形式美.按照太极图的构图方法,在平面直角坐标系中,圆被
的图象分割为两个对称的鱼形图案,其中小圆的半径均为2,现在大圆内随机取一点,则此点取自阴影部分的概率为( )
A. B. C. D.
8.将一枚质地均匀的骰子投两次,得到的点数依次记为和,则方有实数解的概率是( )
A. B. C. D.
9.下表是某单位1~4月份用水量(单位:百吨)的一组数据:
月份
1
2
3
4
用水量
4
5
7
由散点图可知,用水量与月份之间有较好的线性相关关系,其回归方程是,则等于( ) A. 6 B. 6.05 C. 6.2 D. 5.95
10.下列四个命题:
①命题“若,则” 的逆否命题为“若,则”
②“”是“”的必要不充分条件
③若为假命题,则均为假命题
④对于命题,使得,则,使得.
其中,错误的命题个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
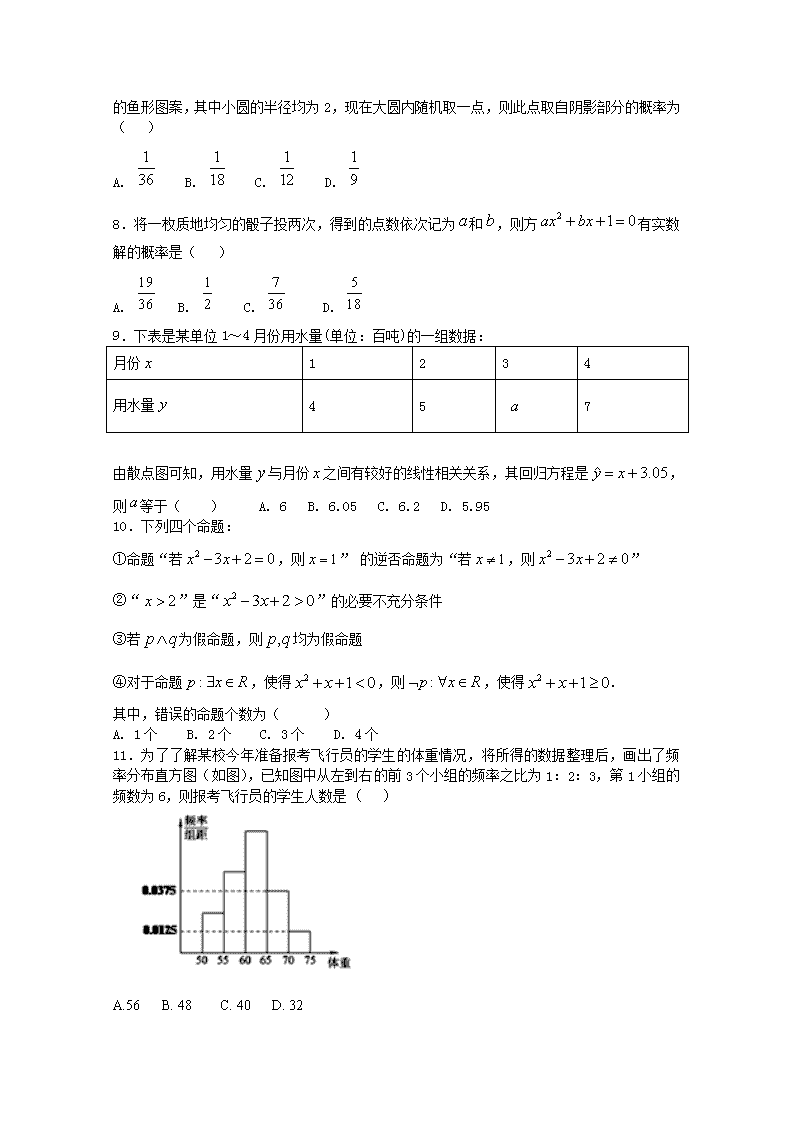
11.为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第1小组的频数为6,则报考飞行员的学生人数是( )
A.56 B. 48 C. 40 D. 32
12.设双曲线的左、右焦点分别为, , ,过作轴的垂线与双曲线在第一象限的交点为,已知, ,点是双曲线右支上的动点,且恒成立,则双曲线的离心率的取值范围是( )
A. B. C. D.
二、填空题(每小题5分,共20分,.将答案填入答卷指定位置).
13.已知向量,且A、B、C三点共线,
则= ________
14.已知抛物线的过焦点的弦为,且,,
则
15.某校开展“爱我漳州、爱我华安”摄影比赛,9位评委为参赛作品A给出的分数如下图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91.复核员在复核时,发现有一个数字(茎叶图中的x)无法看清.若记分员计算无误,则数字x应该是 .
16.设圆的圆心为, 是圆内一定点, 为圆周上任一点,线段的垂直平分线与的连线交于点,则的轨迹方程为________
三.解答题(本大题共6小题,满分70分,解答应写出文字说明,推理过程或演算步骤)
17.已知集合
(1)若,求的概率;
(2)若,求的概率.
18.命题:;命题:方程表示焦点在轴上的椭圆.若“且”是假命题,“或”是真命题,求实数的取值范围.
19.某校高三()班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.
(1)求全班人数及分数在之间的频数,并估计该班的平均分数;
(2)若要从分数在之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在之间的概率.
20.已知为坐标原点, 是椭圆上的点,设动点满足.
(1)求动点的轨迹的方程;
(2)若直线与曲线相交于, 两个不同点,求面积的最大值.
21.如图,是边长为的正方形,平面,,,与平面所成角为.
(Ⅰ)求证:平面.
(Ⅱ)求二面角的余弦值.
(Ⅲ)设点是线段上一个动点,试确定点的位置,使得平面,并证明你的结论.
22.已知椭圆过点,离心率为.
(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线交抛物线于两点, 为原点.
①求证: ;
②设、分别与椭圆相交于、两点,过原点作直线的垂线,垂足为,证明: 为定值.
华安一中2017-2018学年上学期
高二数学(理科)第二次月考试题参考答案
一、选择题:CBACD DDACB BA
二、填空题:13. ; 14. 3 15. ; 16.
三.解答题:
17.(1)设为事件,
,即,即.…………2分
则基本事件有:共个,其中满足的基本事件有个,所以.故的概率为.…………5分
(2)设为事件,因为,则基本事件为如图四边形区域,事件包括的区域为其中的阴影部分. …………7分
所以,…………9分
故的概率为.…………10分
18.命题: 为真,
…………2分
命题为真,即方程是焦点在轴上的椭圆, …………4分
又 “且”是假命题,“或”是真命题
是真命题且是假命题,或是假命题且是真命题…………6分
或 …………10分
的取值范围是…………12分
19.(1)由茎叶图知,分数在之间的频数为,频率为,
全班人数为.…………3分
所以分数在之间的频数为 …………4分
分数在之间的总分为;
分数在之间的总分为;
分数在之间的总分数为;
分数在之间的总分约为;
分数在之间的总分数为;
所以,该班的平均分数为.…………7分
(2)将之间的个分数编号为,之间的个分数编号为,
在之间的试卷中任取两份的基本事件为:
,,,,,,,,,
,,,,,共个,
其中,至少有一个在之间的基本事件有个,
∴至少有一份分数在之间的概率是.…………12分
20.(1)设点,,则由,得,即,
,因为点在椭圆,所以,故,即动点的轨迹的方程为. …………4分
(2)由曲线与直线联立得,消得,
因为直线与曲线交于, 两点,
所以,又,所以
设, ,则, …………8分
因为点到直线: 的距离,…………9分
,…………10分
当且仅当,即时取等号,所以面积的最大值为. …12分
21.(Ⅰ)证明:∵平面,平面,∴ …………1分
又∵是正方形, ∴,…………2分
∵,∴平面.…………3分
(Ⅱ)∵,,两两垂直,所以建立如图空间直角坐标系,
∵与平面所成角为,即 …………4分
∴ 由,可知:,.
则,,,,,
∴,,…………6分
设平面的法向量为,则,即,令,则.
因为平面,所以为平面的法向量,∴,
所以.
因为二面角为锐角,故二面角的余弦值为.…………9分
(Ⅲ)依题意得,设,则,
∵平面,∴,即,解得:,
∴点的坐标为,此时,∴点是线段靠近点的三等分点. ……12分
22. (1) ,所以,又,解得,,
所以椭圆的方程为 …………3分
(2)①证明:设、,
依题意,直线一定有斜率, 的方程为,
联立方程消去得 ,,又,,……7分
②证明:设、,直线的方程为,,,,
联立方程消去得 ,
,,…………9分
而
由 得,即.
所以为定值…………12分