- 623.00 KB
- 2021-06-19 发布
数学试卷(文科)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设是两个命题,若是的充分不必要条件,那么是的( )
A.充分不必要条件 B.必要不充分条件
C.充分且必要条件 D.既不充分又不必要条件
2.抛物线的焦点坐标是( )
A. B. C. D.
3.甲、乙、丙名学生排成一排,其中甲、乙两人站在一起的概率是( )
A. B. C. D.
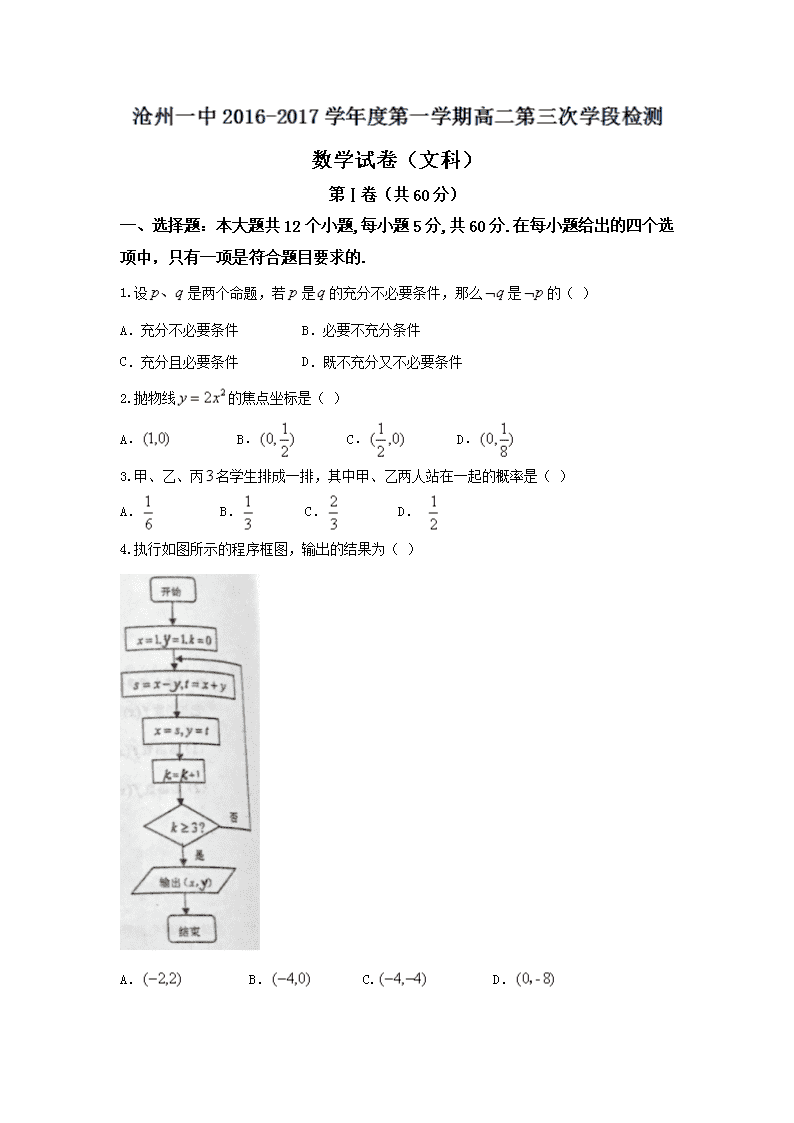
4.执行如图所示的程序框图,输出的结果为( )
A. B. C. D.
5.直线经过椭圆的一个顶点和一个焦点,若椭圆中心到的距离为其短轴长的,则该椭圆的离心率为( )
A. B. C. D.
6.观察下列各式:则的末四位数字为( )
A. B. C. D.
7.椭圆的离心率,则值为( )
A. B.或 C. D.或
8.若函数存在极值,则实数的取值范围是( )
A. B. C. D.
9.已知曲线在处的切线与抛物线相切,则抛物线的准线方程为( )
A. B. C. D.
10.定义在上的函数上的函数满足,且对任意都有,则不等式的解集为( )
A. B. C. D.
11.已知函数,且,则的值是( )
A.正数 B.负数 C.零 D.不能确定符号
12.已知函数,若存在唯一的零点,且,则的取值范围是( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.是双曲线上一点,是双曲线的两个焦点,且,则的值是 .
14.二维空间中圆的一维测度(周长),二维测度(面积),观察发现;三维空间中球的二维测度(表面积),三维测度(体积),观察发现.已知四维空间中“超球”的三维测度,猜想其四维测度 .
15.在平面直角坐标系中,若曲线(为常数)过点,且该曲线在点处的切线与直线平行,则的值是 .
16.设已知抛物线的顶点在坐标原点,焦点为,直线与抛物线相交于两点,若的中点为,则直线的方程为 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. (本小题满分10分)
已知,若是的充分不必要条件,求实数的取值范围.
18. (本小题满分12分)
已知直线与双曲线.
(1) 若,求与相交所得的弦长;
(2)若与有两个不同的交点,求双曲线的离心率的取值范围.
19. (本小题满分12分)
某大学高等数学老师这学期分别用两种不同的教学方式试验甲、乙两个大一新班(人数均为人,入学时的数学平均分数和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各名同学的高等数学期末考试成绩(单位:分),得到如下茎叶图:
(1) 依茎叶图判断哪个班的平均分高(不需要计算);
(2) 现从甲班高等数学成绩不低于分的同学中随机抽取两名同学,求成绩为分的同学至少有一个呗抽中的概率;
(3) 学校规定:成绩不低于分为优秀,请填写下面的列联表,并判断“能否在犯错误的概率不超过的前提下认为成绩优秀与教学方式有关”(的观测值的计算结果小数点后保留三位有效数字)
注:参考数据与公式,其中
临界值表:
20. (本小题满分12分)
已知函数,其中为实数.
(1) 若在处取得的极值为,求的值;
(2)若在区间上为减函数,且,求的取值范围.
21. (本小题满分12分)
已知函数.
(1) 若函数在上是增函数,求实数的取值范围;
(2)若函数在上的最小值为,求实数的值.
22. (本小题满分12分)
已知椭圆的一个顶点为,焦点在轴上,其右焦点到直线的距离为.
(1) 求椭圆的方程;
(2) 设直线,是否存在实数,使直线与椭圆有两个不同的交点,且,若存在,求出的值;若不存在,请说明理由.
高二数学月考题答案(文科)
一、选择题
1-5: ADCBC 6-10:DBADD 11、12:BC
二、填空题
13. 14. 15. 16.
三、解答题
17.解:满足,即或,
满足或,
因为是的充分不必要条件,所以,即.
18. 解:(1) 弦长为
(2)
且
,所以且,
且
19. (1)由图可知乙高
(2) 甲班不低于分的同学有名,所以从这名同学抽取名,有种,分的同学有两名,至少有一名的抽法有种,所以概率为
(3) ,
所以能在犯错误的概率不超过的前提下认为成绩优秀与教学方式有关.
20. 解:(1)
经检验符合题意
(2)
因为函数在区间上为减函数,
所以在区间恒成立,
即,解得.
∴得不符合题意舍
②当时,在成立,∴在区间为减函数,
∴在成立,∴在区间为增函数,
∴(舍)
③当时,在恒成立,∴在区间为减函数,
∴.
22. 解:(1)因为焦点在轴,顶点.设右焦点坐标为,
由题得.
(2) 设
即的中点坐标
∵,∴,∴,经检验不合题意,∴不存在.