- 1008.50 KB
- 2021-06-19 发布
高二(文数)试卷
考试时间:120分钟 满分:150分 命题人:于猛 校对人:宇宁
一、选择题
1.已知集合, ,则 ( )
A. B. C. D.
2.已知函数,若有,则的取值范围是( )
A. B. C. D.
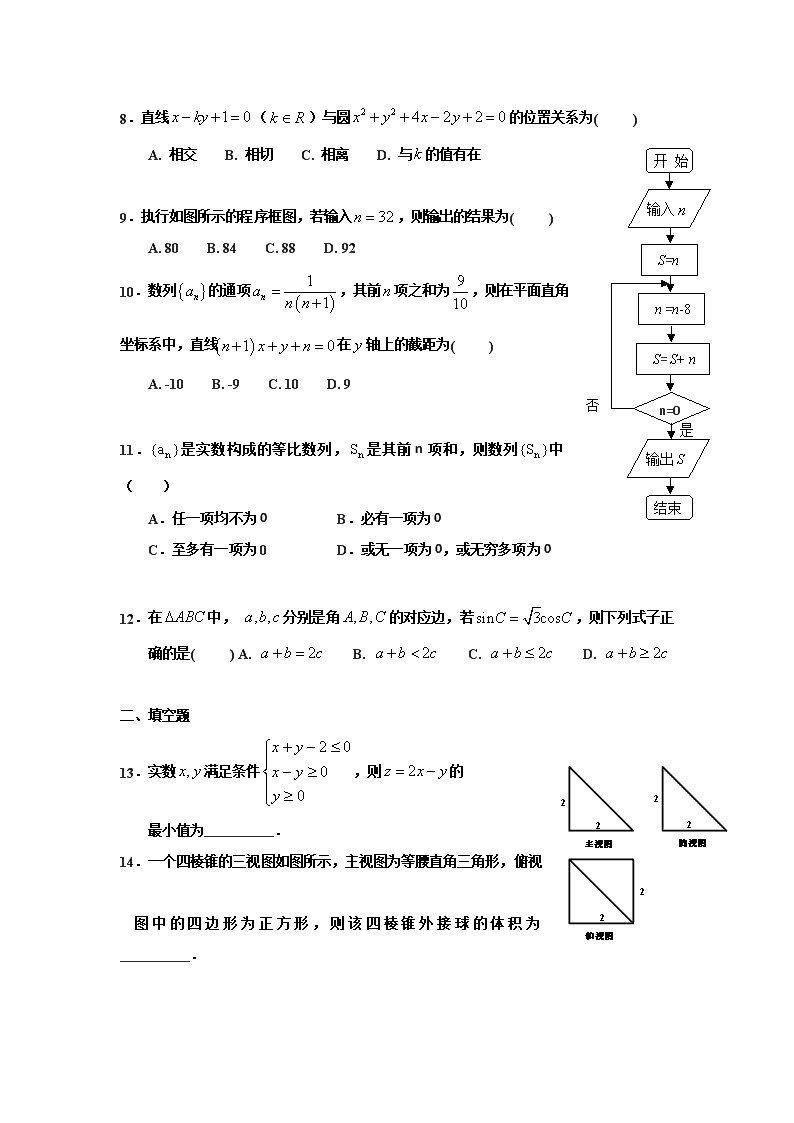
3.设和为不重合的两个平面, 是一条直线,给出下列命题中正确的是( )
A. 若一条直线与内的一条直线平行,则
B. 若平面内有无数个点到平面的距离相等,则
C. 若与内的无数条直线垂直,则
D. 若直线在内,且,则
4.为得到函数的图象,可将函数的图象( )
A. 向右平移个单位 B. 向左平移个单位
C. 向左平移个单位 D. 向右平移个单位
5.已知关于的方程有两个不相等的实数根,则可取的最大整数值为 ( ) A. -1 B. 0 C. 1 D. 2
6.已知等差数列的前项和为,若三点共线, 为坐标原点,且(直线不过点),则等于( )
A. B. C. D.
7.已知等比数列的前项和公式,则其首项和公比分别为( )
A. B. C. D.
8.直线()与圆的位置关系为( )
是
结束
输出S
S= S+ n
S=n
开 始
输入n
n =n-8
n=0
否
A. 相交 B. 相切 C. 相离 D. 与的值有在
9.执行如图所示的程序框图,若输入,则输出的结果为( )
A. 80 B. 84 C. 88 D. 92
10.数列的通项,其前项之和为,则在平面直角坐标系中,直线在轴上的截距为( )
A. -10 B. -9 C. 10 D. 9
11.是实数构成的等比数列,是其前n项和,则数列中( )
A.任一项均不为0 B.必有一项为0
C.至多有一项为0 D.或无一项为0,或无穷多项为0
12.在中, 分别是角的对应边,若,则下列式子正确的是( ) A. B. C. D.
二、填空题
13.实数满足条件,则的
最小值为__________.
14.一个四棱锥的三视图如图所示,主视图为等腰直角三角形,俯视
图中的四边形为正方形,则该四棱锥外接球的体积为__________.
15.已知函数定义域为R,且图象对称中心为,则__________.
16.若不等式对任意恒成立,则实数的取值范围为__________.
三、解答题
17.已知分别是内角的对边, .
(1)若,求
(2)若,且求的面积.
18.已知点,直线及圆
(1)求过点的圆的切线方程;
(2)若直线与圆相交于两点,且弦的长为,求的值.
19.如图,三棱锥P-ABC中,PA平面ABC,.
(Ⅰ)求三棱锥P-ABC的体积;
(Ⅱ)证明:在线段PC上存在点M,使得ACBM,并求的值.
20.已知数列的前项和为,且,又数列满足:.
(1)求数列的通项公式;
(2)当为何值时,数列是等比数列?此时数列的前项和为,若存在,使成立,求的最大值.
21.全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标.根据相关报道提供的全网传播2017年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号
分组
频数
1
2
2
8
3
7
4
3
(Ⅰ)现从融合指数在和内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在内的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
22.已知为正项等比数列,为等差数列的前项和为.
(1)求数列和的通项公式;
(2)设 , 求.
高二 (文数 )参考答案
一、选择题
1.C 2.C 3.D 4.B 5.B 6.B 7.B 8.A 9.A 10.B 11.D 12.C
二、填空题
13.0 14. 15. 68 16.
17.(本题 满分10分)
(1)由题设及正弦定理可得又,可得
由余弦定理可得 ----------------(5分)
(2)由(1)知因为,由勾股定理得故,得所以的面积为1. ----------------(10分)
18.(本题 满分12分) (1)由题意知圆心的坐标为,半径为,
当过点的直线的斜率不存在时,方程为.
由圆心到直线的距离知,此时,直线与圆相切
当过点的直线的斜率存在时,设方程为
即,由题意知,解得.
∴方程为,即.
故过点的圆的切线方程为或. ----------------(6分)
(2)∵圆心到直线的距离为.∴
解得. ----------------(12分)
19.(本题 满分12分) (Ⅰ)
解:由题设=1, 可得.
由面 可知是三棱锥的高,又
所以三棱锥的体积 ----------------(6分)
(Ⅱ)证:在平面内,过点B作,垂足为,过作交于,连接.
由面知,所以.由于,故面,又面,所以.
在直角中,,从而.由,得. ----------------(12分)
20.(本题 满分12分)
(1)由,
当时,;当时,,
故数列的通项公式为 ----------------(4分)
(2)由,则,则数列为等比数列,
则首项为满足的情况,故,----------------(6分)
则.----------------(8分)
因为,所以是单调递增的,故且. -----------(11分)
又存在,使成立,则的最大值为1. ----------------(12分)
21.(本题 满分12分) 解法一:(I)融合指数在内的“省级卫视新闻台”记为,,;融合指数在内的“省级卫视新闻台”记为,.从融合指数在和内的“省级卫视新闻台”中随机抽取家的所有基本事件是:,,,,,,,,,,共个.
其中,至少有家融合指数在内的基本事件是:,,,,,,,,,共个.
所以所求的概率.----------------(6分)
(II)这家“省级卫视新闻台”的融合指数平均数等于.----------------(12分)
解法二:(I)融合指数在内的“省级卫视新闻台”记为,,;融合指数在内的“省级卫视新闻台”记为,.从融合指数在和内的“省级卫视新闻台”中随机抽取家的所有基本事件是:,,,,,,,,,,共个.
其中,没有家融合指数在内的基本事件是:,共个.
所以所求的概率.
(II)同解法一.
22.(本题 满分12分)
(1),又 .---(6分)
(2)
,
相减得
----------------(12分)