- 620.00 KB
- 2021-06-18 发布
南涧县民族中学2017——2018学年上学期期中考
高二数学试题(文科)
班级 姓名 学号
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
注:所有题目在答题卡上做答
第I卷(选择题 共60分)
一、单项选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的。)
1. 已知集合,则 ( )
A. B. C. D.
2.已知实数满足,则的最小值为( )
A. B. C. D.
3.设,,,则( )
A. B. C. D.
4.已知等比数列的公比,则其前2017项和
A. B. C. D.
5.某企业节能降耗技术改造后,在生产某产品过程中记录的产量(吨)与相应的生产能耗(吨)的几组对应数据如下表所示:
3
4
5
6
3
4
若根据表中数据得出关于的线性回归方程为,则表中的值为( )
A. B. C. D.
6.设是等差数列的前项和,若,则( )
A.1 B.2 C.3 D.4
7.【2017届广东湛江二模】下列命题中,正确的是( )
A. 命题:“, ”的否定是“, ”
B. 函数的最大值是
C. 已知,a,b均为实数,则的充要条件是
D. 函数既不是奇函数,也不是偶函数
8.已知三棱锥的各顶点都在同一球面上,且平面,若该棱锥的体积为,,,,则此球的表面积等于( )
A. B. C. D.
9.已知圆M:截直线所得线段的长度是,则圆M与圆N:的位置关系是( )
(A)相交(B)内切(C)外切(D)相离
10.已知函数向左平移个单位后,得到函数,下列关于的说法正确的是( )
A.图象关于点中心对称 B.图象关于轴对称
C.在区间单调递增 D.在单调递减
11.过椭圆的左焦点作轴的垂线交椭圆于点,为右焦点,若,则椭圆的离心率为( )
A. B. C. D.
12.在中,已知,,若点在斜边上,,则的值为 ( ).
A.6 B.12 C.24 D.48
二、填空题(本大题共4小题,每小题5分,共20分)
13.设直线,直线,若,则
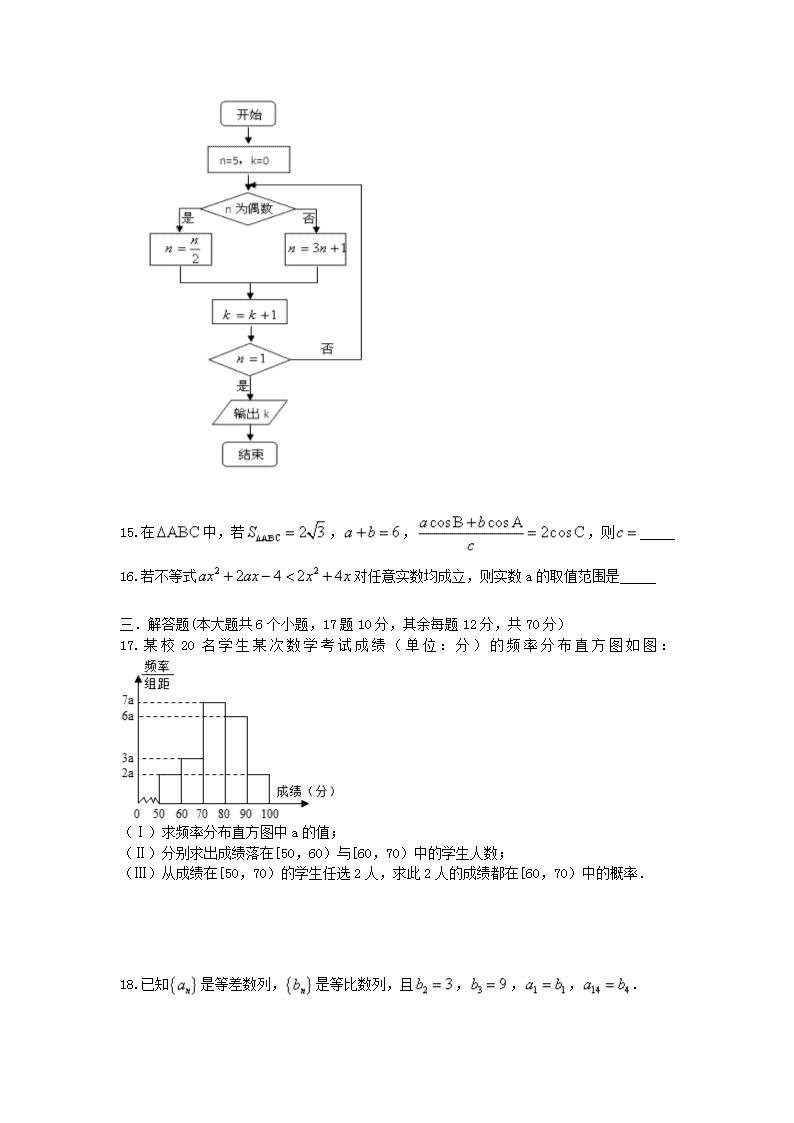
14.执行如图所示的程序框图,输出的k值是
15.在中,若,,,则
16.若不等式对任意实数均成立,则实数a的取值范围是
三. 解答题(本大题共6个小题,17题10分,其余每题12分,共70分)
17.某校20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(Ⅲ)从成绩在[50,70)的学生任选2人,求此2人的成绩都在[60,70)中的概率.
18.已知是等差数列,是等比数列,且,,,.
(1)求的通项公式;
(2)设,求数列的前项和.
19.已知的面积为,且,.
(1)求;
(2)若点为边上一点,且与的面积之比为
求证:;
20.【河北省冀州中学2017届高三(复习班)上学期第二次阶段考试】已知函数.
(Ⅰ)求的最小正周期和单调增区间;
(Ⅱ)若为的一个零点,求的值.
21.如图1,直角梯形,,,,点为的中点,将沿折起,使折起后的平面与平面垂直(如图2).在图2所示的几何体中:
⑴求证:平面;
⑵点在棱上,且满足平面,求几何体的体积.
图1
图2
22.已知椭圆的中心在坐标原点,焦点在轴上,离心率,且椭圆经过点,过椭
圆的左焦点且不与坐标轴垂直的直线交椭圆于,两点.
(1)求椭圆的方程;
(2)设线段的垂直平分线与轴交于点,求△的面积的取值范围.
南涧县民族中学2017——2018学年上学期期中考
高二数学(文科)参考答案
一、 选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
D
A
D
C
B
D
A
C
D
C
二、填空题
13. -7 14. 5
15. 16.
三、解答题(本大题共6小题,共70分)
17:解:(Ⅰ)根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.
(Ⅱ)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
(Ⅲ)记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,则成绩在[50,70)的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个, 其中2人的成绩都在[60,70)中的基本事件有CD,CE,DE共3个,故所求概率为P=.
18:【解析】(1)等比数列的公比,
所以,,
设等差数列的公差为,
因为,,
所以,即,
所以……………………………………………………………………5分
(2)由(1)知,,,
因此,从而数列的前项和
.
19:
20:
21:⑴ …………………………………………1分,
,,
……3分(其他方法求值也参照给分)
∵,
∴() …………………………………………4分
∵平面平面,
平面平面,
∴平面 …………………………………………6分
⑵∵平面,平面,平面平面,
∴ …………………………………………7分
∵点为的中点,
∴为的中位线 …………………………………………8分
由⑴知,几何体的体积…………………10分 …………………………………………11分,
…………………………………………12分
22:
所以的取值范围是.