- 643.50 KB
- 2021-06-02 发布
吉林省梅河口市第五中学2018届高三上学期第三次月考
数学试卷(文科)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设全集,则中整数元素的个数为( )
A. B. C. D.
2.设复数满足,则( )
A. B. C. D.
3.已知向量,则“”是“与反向”的( )
A. 充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.设,定义运算:,则( )
A. B. C. D.
5.① 已知,求证,用反证法证明时,可假设;② 设为实数,,求证与中至少有一个不小于,有反证法证明时可假设,且,以下说法正确的是( )
A.①与②的假设都错误 B.①与②的假设都正确
C.①的假设正确,②的假设错误 D.①的假设错误,②的假设正确
6.若函数在上递减,则的取值范围是( )
A. B. C. D.
7.用数学归纳法证明“”,则当时,应当在时对应的等式的两边加上( )
A. B. C. D.
8.已知对一切都成立,则( )
A. B.
C. D.
9.设满足约束条件,则的取值范围为( )
A. B. C. D.
10.在一次体育兴趣小组的聚会中,要安排人的座位,使他们在如图所示的个椅子中就坐,且相邻座位(如与与)上的人要有共同的体育兴趣爱好,现已知这人的体育兴趣爱好如下表所示,且小林坐在号位置上,则号位置上坐的是( )
A. 小方 B.小张 C.小周 D.小马
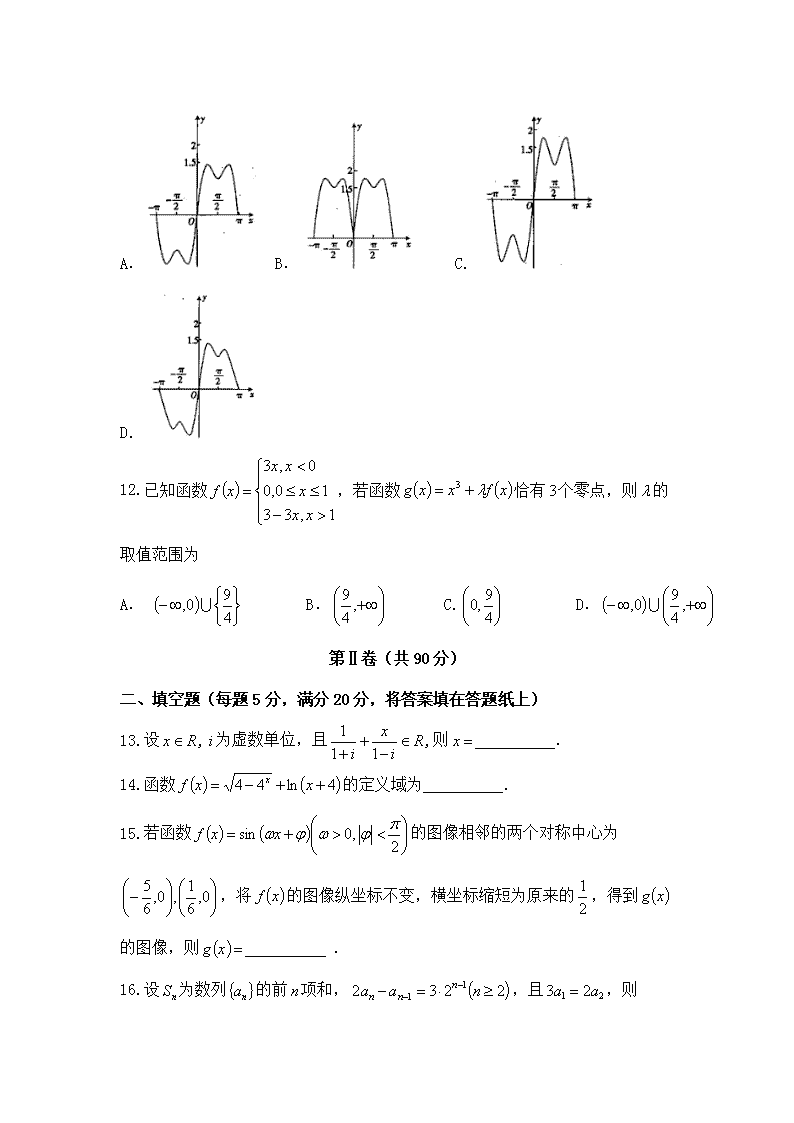
11.函数在上的图像为
A. B. C. D.
12.已知函数,若函数恰有个零点,则的取值范围为
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.设,为虚数单位,且,则 .
14.函数的定义域为 .
15.若函数的图像相邻的两个对称中心为,将的图像纵坐标不变,横坐标缩短为原来的,得到的图像,则 .
16.设为数列的前项和,,且,则
;
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 已知函数
(1)求的最大值,并指出此时的值;
(2)求不等式的解集.
18.已知复数
(1)若,求;
(2)若在复平面内对应的点位于第一象限,求的取值范围.
19.(1) 用分析法证明:当时,;
(2)证明:对任意这个值至少有一个不少于
20.在锐角中,角所对的边分别为,已知
(1)证明:
(2)若的面积为线段的中点,,求.
21.设为数列的前项和,,数列满足
(1)求及;
(2)记表示的个位数字,如,求数列的前项和.
22.已知函数的图像与轴相切,且切点在轴的正半轴上.
(1)若函数在上的极小值不大于,求的取值范围;
(2)设,证明:在上的最小值为定值.
试卷答案
一、选择题
1-5: 6-10: 11、12:
二、填空题
13. 14. 15. 16.
三、解答题
17. 解:(1)
当且仅当即时等号成立,
故的最小值为,此时
(2)由得,又,
,故所求不等式的解集为.
18.解:(1)
若,则
(2)若在复平面内对应的点位于第一象限,则且,
解得,即的取值范围为.
19.解:(1) 要证原不等式成立,只需证成立,
即证:成立,
即证:成立,
即证:成立,
原不等式成立.
(2)假设这个值没有一个不小于,
即,
则, (※)
而,
这与(※)矛盾,所以假设不成立,即原命题成立.
20.解:(1) ,
,
,
,又,得,即
(2)
在中,,
在中,,
又,则,
由,得
21.解:(1) 当时,,
由于也满足,则
是首项为,公差为的等差数列,
(2)的前项依次为,
的前项依次为,
易知,数列与的周期均为,
的前项和为
22.解:(1) 令得,
由题意可得
,
当,即时,无极值,当,即时,令得;
令得或,
在处取得极小值.
当,即时,在上无极小值,
故当时,在上有极小值,
且极小值为,
即
又,
(2),
设,
,又,
在上递增,
令得;令得
为定值.